તળાવના તળિયેથી પરપોટો સપાટી પર આવતા ત્રિજયા બમણી થાય છે. $H$ ઊંચાઇના પાણીના સ્તંભનું દબાણ વાતાવરણ જેટલું હોય,તો તળાવની ઊંડાઇ કેટલી થાય? ( પ્રક્રિયા સમતાપી ધારો )
AIIMS 1995, Diffcult
c
(c) \({P_1}{V_1} = {P_2}{V_2}\)==> \(({P_0} + h + g) \times \frac{4}{3}\pi {r^3}\)=\({P_0} \times \frac{4}{3}\pi {(2r)^3}\)
Where, \(h = \) depth of lake
==> \(h\rho g = 7{P_0}\)==> \(h = 7 \times \frac{{H\rho g}}{{\rho g}} = 7H.\)
(c) \({P_1}{V_1} = {P_2}{V_2}\)==> \(({P_0} + h + g) \times \frac{4}{3}\pi {r^3}\)=\({P_0} \times \frac{4}{3}\pi {(2r)^3}\)
Where, \(h = \) depth of lake
==> \(h\rho g = 7{P_0}\)==> \(h = 7 \times \frac{{H\rho g}}{{\rho g}} = 7H.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાત્રના તળિયે $1 \,cm^{2}$ આડછેદવાળું છિદ્ર છે,પાત્રમાં $70\, cm^{3}/sec$ ના દરથી પાણી નાખતાં મહત્તમ ........ $cm$ ઊંચાઇ સુઘી પાણી ભરી શકાય.View Solution
- 2એક હાઇડ્રોલિક ઑટોમોબાઇલ લિફ્ટ મહત્તમ $3000\, kg$ દળની કારને ઊંચકવા માટે બનાવેલી છે.આ વજન ઊંચકતા પિસ્ટનના આડછેદનું ક્ષેત્રફળ $425\, cm^2$ છે. આ પિસ્ટનને કેટલું મહત્તમ દબાણ સહન કરવું પડશે ?View Solution
- 3એક હાઈડ્રોલિક લીફટની $5000\,kg$ દળના વાહનને ઉંયકવા માટે રચના કરેલી છે. વજન ઉંચકતા નળાકારના આડછેદનું ક્ષેત્રફળ $250\,cm ^2$ છે. નાના પિસ્ટન દ્વારા અનુભવાતુ મહત્તમ દબાણ $........$ છે [$g =10\,m / s ^2$ ધારો.]View Solution
- 4સ્ટોક્સના નિયમની સકાચણી કરવા માટે કરેલા પ્રયોગમાં $r$ ત્રિજ્યા અને $\rho$ ઘનતા ધરાવતા એક ગોળ દડાને પાણી ભરેલા પાત્રમાં પાણીની સપાટીથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે. જો પાણીની અંદર દડાનો ટર્મિનલ વેગ એ પાણીની અંદર આવતા પહેલા દડાના વેગ જેટલો હોય તો ઊંચાઈ $h$ કોના સમપ્રમાણમાં હશે? (હવાનો શ્યાનતાગુણાંક અવગણો)View Solution
- 5જ્યારે તેનો વહન દર $0.18$ લી$/$મિનીટ થી વધારીને $0.48$ લી$/$મિનીટ કરવામાં આવે ત્યારે વર્તુળાકાર નળમાંથી વહેતા પાણીના દહનનો પ્રકાર કયો હો ? ત્રિજ્યા અને પાણીની નિગ્ધતા અનુક્રમે $0.5\, cm$ અને $10^{-3}\, Pa s$ છે.View Solution
(પાણીની ઘનતા : $10^{3}\, kg / m ^{3}$). - 6View Solutionએક નાના સ્ટીલના ગોળાને ગ્લિસરીનથી ભરેલ લાંબા નળાકર પાત્રમાં મુક્ત કરવામાં આવે છે. તો નીચેના માંથી ક્યો આલેખ આ ગોળાની ગતિ માટે વેગ વિરુદૂધ સમયનો આલેખ દર્શાવશે?
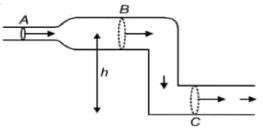
- 7આકૃતિમાં દર્શાવ્યા મુજબ ચેનલમાંથી પાણીનું વહન થઈ રહ્યું છે. (શિરોલંબ સમતલમાં રહેલી) ત્રણ ભાગો $A, B$ અને $C$ દર્શાવેલા છે. $B$ અને $C$ વિભાગ આડછેદનું સમાન ક્ષેત્રફળ ધરાવે છે. જો $P_A, P_B$ અને $P_C$ એ અનુક્રમે $A, B$ અને $C$ પરના દબાણો હોય તોView Solution
- 8$1.0\, m^2$ ક્ષેત્રફળનું ચોરસ તળિયું ધરાવતી એક ટાંકી મધ્યમાં એક ઊર્ધ્વ દીવાલ વડે વિભાજિત કરેલ છે. આ દીવાલના તળિયે એક નાના મિજાગરાવાળું $20\, cm^2$ ક્ષેત્રફળનું બારણું છે. ટાંકીના એક વિભાગમાં પાણી અને બીજામાં ઍસિડ ($1.7$ સાપેક્ષ ઘનતા ધરાવતો) બંને $4.0\, m$ ની ઊંચાઈ સુધી ભરેલ છે. આ બારણાને બંધ રાખવા માટે જરૂરી બળની ગણતરી કરો.View Solution
- 9એકબીજામાં મિશ્રણ ન થઈ શકતા હોય, તેવા પ્રવાહીઓ કે જેમની ઘનતા $\rho$ અને $n\rho ( n>1) $ છે, જે કોઇ પાણીમાં ભરેલાં છે.દરેક પ્રવાહીની ઊંચાઇ $h$ છે. $L$ લંબાઇ અને $ d$ ઘનતાના એક નળાકારને આ પાત્રમાં રાખવામાં આવે,ત્યારે આ નળાકાર આ પાત્રમાં એવી રીતે તરે છે, કે જેથી તેની અક્ષ શિરોલંબ રહે તથા પ્રવાહીમાં તેની લંબાઇ $PL(P < 1)$ રહે છે, તો ઘનતા $d$ કેટલી હશે?View Solution
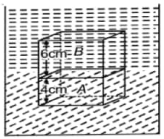
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે બે જુદા-જુદા પ્રવાહીથી $10 \,cm$ બાજુવાળા સમઘનને સમતોલનમાં રાખેલ છે. $A$ અને $B$ ની વિશિષ્ટ ગુરત્વ $0.6$ અને $0.4$ છે. તો સમઘનનું દળ .......... $g$ ?View Solution