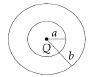
ત્રિજયા $‘a’$ અને ત્રિજયાા $‘b’$ ધરાવતા બે સમકેન્દ્રિય ગોળા ( જુઓ ચિત્ર ) ની વચ્ચેના ભાગમાં વિદ્યુત ઘનતા $\rho = \frac{A}{r}$ છે.જયાં $A$ અચળાંક છે અને કેન્દ્ર થી અંતર $r$ છે. ગોળાઓના કેન્દ્ર પર બિંદુવત વિદ્યુતભાર $Q$ છે.ગોળાઓનના વચ્ચેના ભાગમાં વિદ્યુતક્ષેત્ર અચળ રહે તે માટેના $A$ નું મૂલ્ય છે.

JEE MAIN 2016, Diffcult
c
Applying Gauss's law
Applying Gauss's law
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{Q}{\epsilon_{0}}\)
\(\therefore \mathrm{E} \times 4 \pi \mathrm{r}^{2}=\frac{\mathrm{Q}+4 \pi \mathrm{ar}^{2}-4 \pi \mathrm{Aa}^{2}}{\epsilon_{0}}\)
\(\rho=\frac{\mathrm{d} \mathrm{r}}{\mathrm{d} \mathrm{v}}\)
\(Q=\rho 4 \pi r^{2}\)
\(\mathrm{Q}=\int_{\mathrm{a}}^{\mathrm{A}} \frac{\mathrm{A}}{\mathrm{r}} 4 \pi \mathrm{r}^{2} \mathrm{dr}=4 \pi \mathrm{A}\left[\mathrm{r}^{2}-\mathrm{a}^{2}\right]\)
\(\mathrm{E}=\frac{1}{4 \pi \epsilon_{0}}\left[\frac{\mathrm{Q}-4 \pi \mathrm{Aa}^{2}}{\mathrm{r}^{2}}+4 \pi \mathrm{A}\right]\)
For \(\mathrm{E}\) to be independent of \('{r}'\)
\(\mathrm{Q}-2 \pi \mathrm{Aa}^{2}=0\)
\(\therefore A=\frac{Q}{2 \pi a^{2}}\)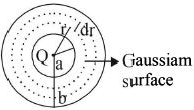
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉગમબિંદુ પર રહેલા વિસ્તરતું કદ $2 \times 10^{-9} \,{m}^{3}$ માં રહેલો વિદ્યુતભાર ...... $nC$ હશે, જો તેના વિદ્યુતક્ષેત્રની વિદ્યુતફ્લક્સ ઘનતા $D=e^{-x} \sin y \hat{i}-e^{-x} \cos y \hat{j}+2 z \hat{k}\, C / m^{2}$ હોય.View Solution
- 2View Solutionઈલેકટ્રોન અને પ્રોટોન સમાન વિદ્યુતક્ષેત્રમાં મૂકેલા છે. તેઓના પ્રવેગનો ગુણોત્તર ...... છે.
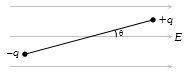
- 3$L$.લંબાઇના સમાન દ્રવ્યમાન રહિત સળિયાના બંને છેડાઓ પર $m$ દળ અને $+q$ તથા $-q$ વીજભાર ઘરાવતા બે બિંદુવત દ્રવ્યમાનો જોડેલ છે. આ રચનાને $E$ તીવ્રતા ઘરાવતા સમાન વિધુતક્ષેત્ર સાથે સૂક્ષ્મ ખૂણેા બનાવે તો સળિયાને વિધુતક્ષેત્ર સાથે સમાંતર થવા માટે કેટલો સમય લાગે?View Solution
- 4$\overrightarrow{ p }$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલના કેન્દ્રથી $r$ અંતરે વિષુવવૃતીય સમતલ પર રહેલા બિંદુ આગળ વિધુતક્ષેત્ર ........... મળે ($r >>$ ડાઈપોલના બે વિધુતભાર વચ્ચેનું અંતર,$\varepsilon_{0}$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
- 5કેન્દ્ર $O$ પર વિદ્યુતક્ષેત્ર કઈ દિશામાં હશે?View Solution

- 6બે સમાન ગોળાઓ સમાન વિદ્યુતભારથી વિદ્યુતભારિત થયેલા છે અને તેમની વચ્ચે લાગતું બળ $F$ છે. જો એક ગોળાનો $50\%$ જેટલો વિદ્યુતભાર બીજા ગોળા પર વહન પામે તો નવું બળ ........ $F$ હશે.View Solution
- 7નાના કદમાં વિદ્યુતભારનું વિતરણ કરેલ છે તો સમગ્ર વિદ્યુતભારને ઘેરતા $10\, cm$ ત્રિજ્યા ગોળાકાર સપાટી પર ફલક્સ $20\, Vm$ છે તો સમકેન્દ્રીય $20\, cm$ ત્રિજ્યાવાળી ગોળાકાર સપાટી માંથી નીકળતુ ફલક્સ .........$Vm$ થાય?View Solution
- 8મિલકનના ઓઇલ ડ્રોપ પ્રયોગમાં એક વિજભાર ટર્મિનલ વેગ $V$ થી ગતિ કરે છે. જો $E$ જેટલું વિદ્યુતક્ષેત્ર શિરોલંબ દિશામાં ઉપર તરફ લગાવવામાં આવે તો તે ઉપર તરફ $2V$ જેટલા ટર્મિનલ વેગથી ગતિ કરે છે. જો વિદ્યુતક્ષેત્રનું મૂલ્ય ઘટાડીને $\frac{E}{2}$ કરવામાં આવે તો આ ટર્મિનલ વેગ કેટલો થાય?View Solution
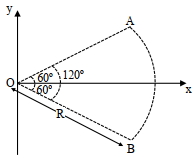
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે સળિયા ${AB}$ ને $120^{\circ}$ ના ખૂણે વાળીને $R$ ત્રિજયાની છાપ બનાવવામાં આવે છે. $(-Q)$ વિદ્યુતભારને સળિયા $AB$ પર સમાન રીતે વિતરિત કરેલ છે. તેના કેન્દ્ર $O$ પર વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ કેટલું હશે?View Solution
- 10$+q$ અને $-q$ વિદ્યુતભાર ધરાવતા બે કણને અમુક અંતરે મૂકતાં તેમની વચ્ચે લાગતું બળ $F$ છે.બંને કણની વચ્ચે $+q$ વિદ્યુતભાર ધરાવતા કણ મૂકવાથી તેના પર કેટલું બળ લાગે?View Solution
