નાના કદમાં વિદ્યુતભારનું વિતરણ કરેલ છે તો સમગ્ર વિદ્યુતભારને ઘેરતા $10\, cm$ ત્રિજ્યા ગોળાકાર સપાટી પર ફલક્સ $20\, Vm$ છે તો સમકેન્દ્રીય $20\, cm$ ત્રિજ્યાવાળી ગોળાકાર સપાટી માંથી નીકળતુ ફલક્સ .........$Vm$ થાય?
Easy
a
ગાઉસના નિયમ મુજબ \(q\) વિદ્યુતભારને દોરતી બંધ સપાટીમાંથી બહાર આવતુ ફલકસ, \(\phi \,\, = \,\,\oint {\mathop E\limits^ \to .d\mathop S\limits^ \to } \,\, = \,\,\frac{q}{{{\varepsilon _0}}}\)
ઉપરના સમીકરણ પરથી સ્પષ્ટ છે કે બંધ સપાટી સામે સંકળાયેલ ફલકસ ફક્ત તેમાં રહેલ વિદ્યુતભાર પર આધાર રાખે છે તથા સપાટીના આકાર અને કદ પર આધાર રાખતી નથી.
ગાઉસના નિયમ મુજબ \(q\) વિદ્યુતભારને દોરતી બંધ સપાટીમાંથી બહાર આવતુ ફલકસ, \(\phi \,\, = \,\,\oint {\mathop E\limits^ \to .d\mathop S\limits^ \to } \,\, = \,\,\frac{q}{{{\varepsilon _0}}}\)
ઉપરના સમીકરણ પરથી સ્પષ્ટ છે કે બંધ સપાટી સામે સંકળાયેલ ફલકસ ફક્ત તેમાં રહેલ વિદ્યુતભાર પર આધાર રાખે છે તથા સપાટીના આકાર અને કદ પર આધાર રાખતી નથી.
\(\phi \,\, = \,\,\oint {\mathop E\limits^ \to .d\mathop S\limits^ \to } \,\, = \,\,\frac{q}{{{\varepsilon _0}}}\,\, = \,\,20\,Vm\) આપેલ છે
\(q/\varepsilon _0\) જ્યાં સુધી ઘેરાયેલ વિદ્યુતભાર અચલ રહેશે ત્યાં સુધી અચળ છે.
માટે સમકેન્દ્રીય \(20\, cm\) ત્રિજ્યામાંથી ફલક્સ = \(20 \,Vm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$Y$ અક્ષ પર $10^3 \,V/m$ ની સમાન વિદ્યુતક્ષેત્રની ક્ષમતા વિતરણ પામેલી છે. $1\, g$ દળ અને $10^{-6} \,C$ વિદ્યુતભાર વાળો એક પદાર્થ ધન $x$ -અક્ષની દિશામાં ઉગમબિંદુથી ક્ષેત્રમાં $10\,m/s$ ના વેગથી પ્રક્ષેપણ કરે છે. $10\ s$ પછી તેની ઝડપ $m/s$ માં ........ છે.View Solution
- 2View Solutionહાઇડ્રોજન જેવા તંત્રમાં, ઇલેક્ટ્રોન અને પ્રોટોન વચ્ચેનાં કુલ્મબિય બળ અને ગુરુત્વકર્ષણ બળનો ગુણોત્તર . . . . .ના ક્રમનો હોય છે.
- 3$E = 3 \times 10^6\ V/m$ ના ક્ષેત્રએ હવાના માધ્યમનું ભંજન બને છે. મહત્તમ વિદ્યુતભાર ......$mc$ કે જે $6\ m$ વ્યાસના ગોળાને આપી શકાય. (કુલંબમાં)View Solution
- 4બે વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $P$ અને $64 \,P$ છે.આ બંને ડાયપોલને વિરુધ્ધ દિશામાં $25 \,cm$ અંતરે મૂકેલા છે.તો $P$ ડાયપોલ મોમેન્ટવાળા ડાયપોલથી કેટલા......$cm$ ના અંતરે વિદ્યુતક્ષેત્ર શૂન્ય થાય?View Solution
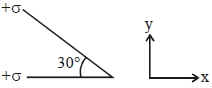
- 5બે $+\sigma$ પૃષ્ઠ વિજભાર ઘનતા ધરાવતા અનંત સમતલને એક બીજા સાથે $30^{\circ} $ ના ખૂણે મૂકવામાં આવે છે, તો તેમની વચ્ચેના ક્ષેત્રમાં વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 6ક્રમિક $ + Q$ અને $ - Q$ વિજભાર ધરાવતા બે બિંદુવત વિજભારો $A$ અને $B$ ને એક બીજાથી નિયત અંતર પર અલગ રાખેલ છે કે જેથી તેમના વચ્ચે લાગતું બળ $F$ છે. જો $A$ નો $25\%$ વિજભાર $B$ પર ટ્રાન્સફર કરવામાં આવે, તો આ વિજભારો વચ્ચે લાગતું બળ કેટલું થશે?View Solution
- 7$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 8View Solutionસમાન રીતે ભારીત અવાહક ધનગોળાના વીજક્ષેત્રના ફેરફારને વિવિધ બિંદુઓ આધારીત આલેખીય રીતે દર્શાવી શકાય છે.
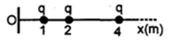
- 9View Solutionનીચે આપેલ આકૃતિમાં ઊગમબિંદુ આગળ અનંત સંખ્યાના વિદ્યુતભારને લીધે વિદ્યુતક્ષેત્રની ગણતરી કરો.
- 10$L$ બાજુવાળા સમઘન $(A\,B\,C\,D\,E\,F\,G\,H)$ ના કેન્દ્ર પર $q$ વિદ્યુતભાર મૂકવામાં આવે છે. કેન્દ્ર $O$ થી $L$ અંતરે $q$ વિદ્યુતભાર મૂકવામાં આવે છે. $BGFC$ માંથી પસાર થતું વિદ્યુતફ્લક્સ કેટલું હશે?View Solution