$V _{ CM }=2\; m / s , m =2\;kg , R =4 \;m$ જ્યારે રીંગ સંપૂર્ણ ગબડે ત્યારે તેનું કોણીય વેગમાન ઉદગમબિંદુને અનુલક્ષીને ($kgm ^{2} / s$ માં)
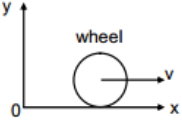
AIIMS 2019, Medium
Download our app for free and get started
a
The moment of inertia about centre of mass is,
The moment of inertia about centre of mass is,
\(I_{C M}=M R^{2}\)
The angular velocity of the wheel is,
\(\omega=\frac{V_{C M}}{R}\)
\(\omega=\frac{2}{4}=0.5 rad / s\)
The angular momentum of the ring about origin is,
\(\vec{L}=I_{C M} \omega+m V_{C M} R\)
\(=2 \times 16 \times 0.5+2 \times 2 \times 4\)
\(=16+16\)
\(=32 \;kg \cdot m ^{2} / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$5\ kg$ દળ ધરાવતા સ્થિર પૈડા પર $30\ Nm $ જેટલું ટૉર્ક $15 $ સેકન્ડ માટે લગાડવામાં આવે છે. પૈડાની જડત્વની ચાકમાત્રા $2\ kg\ m^2$ છે. આ $10$ સેકન્ડમાં પૈડાએ કરેલું કોણીય સ્થાનાંતર ....... $\ rad$View Solution
- 2નીચે આપેલા પદાર્થોને એક ઢાળ પર નીચેથી ઉપર તરફ (સરક્યાં વગર) ભ્રમણ કરવવામાં આવે છેView Solution
$(i)$ $R$ ત્રિજ્યાની રિંગ
$(ii)$ $\frac {R}{2}$ ત્રિજ્યાનો ઘન નળાકાર અને
$(iii)$ $\frac {R}{4}$ ત્રિજ્યાનો ઘન ગોળો
જો ઢાળના તળિયે બધાના દ્રવ્યમાન કેન્દ્રનો વેગ સમાન હોય તો તેમના દ્વારા પ્રાપ્ત થતી મહત્તમ ઊંચાઈનો ગુણોત્તર કેટલો થાય?
- 3બે સમાન તકતીના સમતલ એકબીજાને લંબ છે.તેમની કોણીય ઝડપ $3 \,rad/sec $અને $4\,rad/sec$ છે.તો તંત્રની પરિણામી કોણીય ઝડપ ........ $rad/sec$ થાય.View Solution
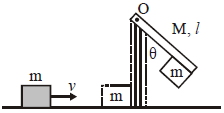
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $m =1\, kg$ દળનો એક પદાર્થ $v=6\, m / s$ જેટલા વેગથી એક ઘર્ષણરહિત સપાટી પર ગતિ કરીને એક સળિયા સાથે અથડાયને તેની સાથે જોડાય જાય છે. આ સળિયો $O$ બિંદુ સાથે જડેલ છે અને અથડામણના કારણે તે $\theta$ ખૂણો બનાવે છે. જો સળિયાનું દળ $M =2 \,kg $ અને લંબાઈ $l=1\, m $ હોય તો $\theta$ ખૂણાનું મૂલ્ય કેટલું હશે?View Solution
$(\left.g=10 \,m / s ^{2}\right)$
- 5બે દળો $ m_1$ અને $m_2$ ને એકબીજાથી $ r $ અંતરે મૂકેલા છે. તંત્રના દ્રવ્યમાન કેન્દ્રમાંથી પસાર થતી અક્ષમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા શોધો.View Solution
- 6View Solutionપદાર્થના બધા જ કણો વર્તૂળાકાર પથમાં ગતિ કરે છે. જ્યારે તેની ભ્રમણ અક્ષ.........
- 7ઓટોમોબાઈલ એન્જિનમાં $ 6000\ rpm$ એ $ 200\ hp$ પાવર મળે છે તેને અનુરૂપ ટોર્ક ......... $N.m$ થશે.View Solution
- 8$M $ દળ તથા $ L$ લંબાઈના સળીયાની તેના એક છેડેથી $L/4$ અંતરે સળીયાની લંબાઈને લંબ અક્ષની આસપાસ જડત્વની ચાકમાત્રા = .....View Solution
- 9બે સમઅક્ષીય તકતી જેની જડત્વની ચાકમાત્રા અનુક્રમે $I_1$ અને $I_2$ છે જે અનુક્રમે $\omega_1$ અને $\frac{\omega_1}{2}$ કોણીય વેગથી તેમની સામાન્ય અક્ષને અનુલક્ષીને ભ્રમણ કરે છે. જ્યારે તેમને એકબીજાના સંપર્કમાં લાવવામાં આવે ત્યારે તે સમાન કોણીય વેગથી ગતિ કરે છે. જો $E_f$ અને $E_i$ તેમની અંતિમ અને શરૂઆતની કુલ ઉર્જા હોય તો $(E_f -E_i)$ કેટલું થાય?View Solution
- 10નિયમિત ઘનતાનો એક નાનો પદાર્થ પ્રારંભિક વેગ $v$ સાથે વક્ર સપાટી પર ઉપર તરફ ગબડે છે. પદાર્થ તેની પ્રારંભિક સ્થિતિની સાપેક્ષે $3v^2/4g$ મહત્તમ ઊંચાઈ સુધી પહોંચે છે. પદાર્થ કયો હશે?View Solution