$V$ કદનું પ્રવાહી મિશ્રાણ એ $\alpha$ અને $\beta$ ઘનતાઓ સાથેના બે પ્રવાહીઓ ધરાવે છે. જો મિશ્રણની ઘનતા $\sigma$ છે તો આ મિશ્રણમાં પહેલા પ્રવાહીનું દળ .......
Diffcult
c
Let mass of liquid with density \(\alpha= M _1\)
Let mass of liquid with density \(\alpha= M _1\)
mass of liquid with density \(\beta= M _2\)
Total volume \(= V\)
Net density of mixture \(=\sigma\)
Total mass \(= M _1+ M _2\)
\(\Rightarrow V \sigma= M _1+ M _2\)
\(\Rightarrow M _2= V \sigma- M _1 \ldots \ldots(1)\)
\(\left[\because \frac{\text { Total Mass }}{ v }=\sigma\right]\)
\(T=\frac{T \text { otal mass }}{\text { Total volume }}=\frac{M_1+M_2}{\frac{M_1}{\alpha}+\frac{M_2}{\beta}} \ldots \ldots \text { (2) }\)
sub \((1)\) in \((2)\)
\(\Rightarrow \sigma=\frac{ M _1+\left( v \sigma- M _1\right)}{\frac{ M _1}{\alpha}+\left(\frac{ v \sigma- M _1}{\beta}\right)}\)
\(\Rightarrow M _1=\frac{\alpha V (\beta-\sigma)}{\beta-\alpha} \text {. }\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જમણી બાજુના આડછેદનો વ્યાસ , ડાબી બાજુના આડછેદનો વ્યાસ કરતાં $n $ ગણો છે.સાંકડી બાજુમાં $ h$ ઊંચાઇ સુધી પાણી ભરેલ છે,જમણી બાજુમાં મરકયુરી ઊંચાઇ કેટલી વધે? ($s =$ મરકયુરીની સાપેક્ષ ઘનતા અને$\rho $ $= $ પાણીની ધનતા )View Solution

- 2View Solutionએક નાના સ્ટીલના ગોળાને ગ્લિસરીનથી ભરેલ લાંબા નળાકર પાત્રમાં મુક્ત કરવામાં આવે છે. તો નીચેના માંથી ક્યો આલેખ આ ગોળાની ગતિ માટે વેગ વિરુદૂધ સમયનો આલેખ દર્શાવશે?
- 3એકબીજામાં મિશ્રણ ન થઈ શકતા હોય, તેવા પ્રવાહીઓ કે જેમની ઘનતા $\rho$ અને $n\rho ( n>1) $ છે, જે કોઇ પાણીમાં ભરેલાં છે.દરેક પ્રવાહીની ઊંચાઇ $h$ છે. $L$ લંબાઇ અને $ d$ ઘનતાના એક નળાકારને આ પાત્રમાં રાખવામાં આવે,ત્યારે આ નળાકાર આ પાત્રમાં એવી રીતે તરે છે, કે જેથી તેની અક્ષ શિરોલંબ રહે તથા પ્રવાહીમાં તેની લંબાઇ $PL(P < 1)$ રહે છે, તો ઘનતા $d$ કેટલી હશે?View Solution
- 4એક પૂર્ણ રીતે ભરેલા બોઈગ વિમાનનું દળ $5.4 \times 10^5\,kg$ છે. તેની પાંખોનું કુલ ક્ષેત્રફળ $500\,m ^2$ છે. તે $1080\,km / h$ ની ઝડપે લેવલ (સમક્ષિતિજ) ઉડ્ડયન સ્થિતિમાં છે. જો હવાની ધનતા $1.2\,kg m ^{-3}$ હોય તો વિમાનની ઉપરની સપાટી આગળ, તેની નીચેની સપાટીની સરખામણીમાં, હવાની ઝડપમાં પ્રતિશત આાંશિક વધારો $.........$ થશે. $(g=10\;m / s ^2)$View Solution
- 5નળાકાર ટયુબ $AB$ માં $ A$ છેડે પાણી ${v_1}$ વેગથી દાખલ થાય છે, અને $ B$ છેડે પાણી ${v_2}$ વેગથી બહાર આવે છે,પ્રથમ કિસ્સા $I$ માં નળી સમક્ષિતિજ રાખેલ છે,બીજા કિસ્સા $ II $ માં નળીનો $ A $ છેડો ઉપર રહે,તેમ શિરોલંબ રાખેલ છે,ત્રીજા કિસ્સા $ III $ માં નળીનો $B $ છેડો ઉપર રહે,તેમ શિરોલંબ રાખેલ છે.તો કયા કિસ્સા માટે ${v_1} = {v_2}$ થાય?View Solution
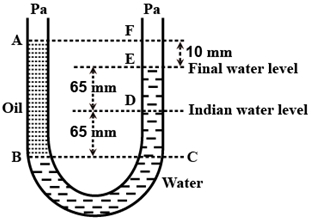
- 6એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution
- 7$20 \,m$ પાણીની સપાટીની નીચે તરવૈયા ઉપર લાગતું દબાણ ............. $atm$View Solution
- 8View Solutionબર્નુલીનો નિયમ કોના સંરક્ષણના નિયમ પર આધાર રાખે છે.
- 9પાણીની સપાટીથી વસ્તુને $2\, km$ ઊંડાઇએ રાખતા તેના કદમાં થતો ફેરફાર $\frac{\Delta V }{ V }=1.36\, \%,$ હોય તો તેના કદ પ્રતિબળ અને કદ વિકૃતિ નો ગુણોત્તર કેટલો થાય?[પાણીની ઘનતા $=1000\, kg m ^{-3}$ અને $\left. g =9.8 \,ms ^{-2} .\right]$View Solution
- 10એક ટાંકીએ પાણીથી ભરવામાં આવી છે અને તેની અંદર બે છિદ્રો $A$ અને $B$ પાડવામાં આવે છે. સમાન અવધિ મેળવવા માટે $\frac{h}{h^{\prime}}$ નો ગુણોત્તર કેટલો હોવો જોઇએ ?View Solution