$V_0$ વોલ્ટેજ એક વિધુત બલ્બ (ગોળો), $P_0$ પાવર આપે છે. જો વોલ્ટેજ $V$ હોય તો તે …$P$ પાવર આપે છે.
Easy
d
Power in resistor is given by
Power in resistor is given by
\(P =\frac{ V ^2}{ R } \text { so } R =\frac{ V ^2}{ P }\)
Now since the bulb is operating initially at Power \(P_0\) and Voltage \(V_0\). So
\(P_0=\frac{V_0^2}{R}\)
Resistance of bulb is \(R =\frac{ V _0^2}{ P _0}\)
now the bulb is attached to voltage \(V\) and it consumes power \(P\) now. So Using value of \(R\) from equation \((1)\)
\(P=\frac{V^2}{R}=\frac{V^2 P_0}{V_0^2}=\left(\frac{V}{V_0}\right)^2 P_0\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ત્રણ અવરોધો $A =2\; \Omega, B =4 \;\Omega, C =6 \;\Omega$ નું સૌથી યોગ્ય સંયોજન કયું હશે કે જેથી આ સંયોજનનું સમતુલ્ય અવરોધ $\left(\frac{22}{3}\right) \Omega$ થાય $?$View Solution
- 2કોષને પોટેન્શિયોમીટર સાથે જોડતાં $ 125\, cm $ લંબાઇએ તટસ્થ બિંદુએ મળે છે.હવે $2\,Ω$ ના અવરોધને કોષ સાથે સમાંતરમાં જોડતાં $ 100\,cm $ લંબાઇએ તટસ્થ બિંદુએ મળે છે.તો કોષનો આંતરિક અવરોધ કેટલા ................ $\Omega$ હશે?View Solution
- 3કોષનો $e.m.f.$ માપવા વોલ્ટમીટર કરતાં પોટેન્શિયોમીટરની પસંદગી વધારે યોગ્ય છે તેના માટેના કારણો નીચે આપેલા છેView Solution
$(i)$ પોટેન્શિયોમીટરમાં કોષમાં કોઈ પ્રવાહ વહેતો નથી.
$(ii)$ પોટેન્શિયોમીટરની લંબાઈના કારણે વધારે સચોટ મૂલ્ય મળે.
$(iii)$ પોટેન્શિયોમીટર દ્વારા ઝડપથી માપન થઈ શકે.
$(iv)$ પોટેન્શિયોમીટરનો ઉપયોગ કરતી વખતે ગેલ્વેનોમીટરની સંવેદિતાથી કોઈ ફરક પડતો નથી
ઉપર પૈકી કયા કારણો સાચા છે?
- 4મીટરબ્રીજની બે ભુજાઓના અવરોધો અનુક્રમે $5\,\Omega$ અને $R\,\Omega$ છે. જયારે અવરોધ $R $ ની સાથે સમાન અવરોધનો શંટ જોડતાં નવો બેલેન્સ પોઇન્ટ $1.6 l_1 $ મળે છે. અવરોધ $R=$ .................. $\Omega$View Solution
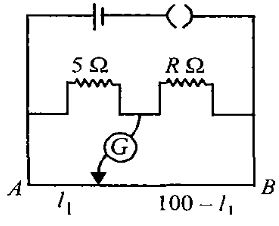
- 5મીટરબ્રિજના પ્રયોગ માટે પરિપથ અને ટેબલ આપેલ છેView Solution
$Sl$. $No$. $R\, (\Omega )$ $l\, (cm)$ $1$. $1000$ $60$ $2$. $100$ $13$ $3$. $10$ $1.5$ $4$. $1$ $1.0$ ઉપર પૈકી કયું અવલોકન ખોટું પડે?
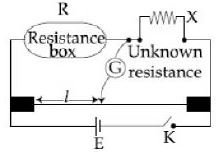
- 6View Solutionઉર્જાનો સ્ત્રોત કોઈ અવરોધ માટે અચળ પ્રવાહ આપે જો તેનો આંતરિક અવરોધ .....
- 7$10\, V$ નો $e.m.f.$ અને $0.5\, ohm$ આંતરિક અવરોધ ધરાવતી બેટરીને એક ચલિત અવરોધ $R$ સાથે જોડેલ છે. $R$ ના કયા મૂલ્ય ($ohm$ માં) માટે તેમાંથી મહત્તમ પાવર પસાર થાય?View Solution
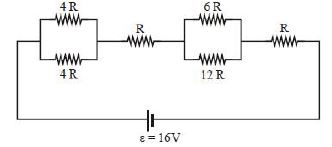
- 8નીચે આપેલ પરિપથને $16\, V$ ના $D.C.$ પ્રવાહ સાથે જોડેલ છે.જો પરિપથ દ્વારા વપરાતો પાવર $4\, Watt$ હોય તો અવરોધ $R$ નું મૂલ્ય કેટલા ................ $\Omega$ હશે?View Solution
- 9$R$ અવરોધ ધરાવતા તારને વચ્ચેથી $180^o$ ના ખુણે વાળી અને બંને છેડે વળ ચડાવવામાં આવે છે જેથી તેની લંબાઈ ટૂંકી થાય તો આ નવા તારનો અવરોધ કેટલો થશે?View Solution
- 10એક પોલા નળાકાર વાહકની લંબાઇ $3.14\,m$ છે જ્યારે તેની આંતરિક અને બાહ્ય વ્યાસ અનુક્રમે $4\,mm$ અને $8\,mm$ છે.વાહકનો અવરોધ $n \times 10^{-3}\,\Omega$ છે.જો દ્રાવ્યની અવરોધકતા $2.4 \times 10^{-8}\,\Omega m$ હોય તો $n$ નું મૂલ્ય $............$ છે.View Solution
