$x$ - અક્ષ પર ગતિ કરી રહેલા કણોનો પ્રારંભિક વેગ $u\;(t= 0$ અને $x=0$ ) છે અને તેનો પ્રવેગ $a=k x$ દ્વારા આપવામાં આવે છે. નીચેનામાંનું ક્યું સમીકરણા તેની વેગ $(v)$ અને સ્થાન $(x)$ ની માટે સાચું છે?
Medium
Download our app for free and get started
c
(c)
(c)
$a=k x \text { and } \frac{v d v}{d x}=a$
$\Rightarrow \int \limits_u^v v d v=\int \limits_0^x a d x=\int \limits_0^x k x d x$
$\left.\Rightarrow \frac{v^2}{2}\right|_u ^v=\left.\frac{k x^2}{2}\right|_0 ^x$
$\Rightarrow v^2-u^2=k x^2 \Rightarrow v^2=u^2+k x^2$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેનામાંથી કયો સ્થાનતર $(X)$ નો સમય સાથેનો ગ્રાફ શક્ય નથી?View Solution
- 2$80 \,m$ ની ઉંચાઈની મકાનની ટોચ પરથી બોલ નીચે ફેંકવામાં આવ્યો છે. આ જ ક્ષણ પર બીજો બોલ મકાનના તળિયેથી $50 \,m / s$ ની ઝડપ સાથે ઉપરની તરફ ગતિ કરે છે. ........ સેકેન્ડે પર બંને બોલ મળશે ?View Solution
- 3એક કણનું સ્થાન $x=\left(5 t^2-4 t+5\right) m$ મુજબ સમય સાથે સંબંધ ધરાવે છે. તો $t=2\,s$ વખતે કણના વેગનું મૂલ્ય $.........\,ms^{-1}$ થશે.View Solution
- 4$A $ પદાર્થ $a_1$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે,અને $2 sec$ પછી $B$ પદાર્થ $a_2$ પ્રવેગથી સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરે છે.જો બંનએ $5^{th}\, sec$ માં કાપેલ અંતર સમાન હોય તો ${a_1}:{a_2}=$View Solution
- 5એક પારિમાણિક ગતિ કરતા એક કણના સ્થાન $x$ અને સમય $t $ વચ્ચેનો સંબંધ નીચે મુજબ છે. $t = \sqrt x + 3$ અહી, $x$ મીટરમાં અને $t$ સેકન્ડમાં છે. જયારે કણનો વેગ શૂન્ય થાય, ત્યારે કણનું સ્થાનાંતર ........ $m$ છે.View Solution
- 6એક પદાર્થ $x=0$ સ્થાને સ્થિર સ્થિતિમાં છે. તે $t=0$ સમયે ધન $x$ દિશામાં અચળ પ્રવેગી ગતિ શરૂ કરે છે. આ જ સમયે બીજો એક પદાર્થ પણ $x =0$ સ્થાનેથી ધન $x$ દિશામાં અચળ ઝડપથી ગતિ કરે છે. $t$ સમય પછી પ્રથમ પદાર્થનું સ્થાન $x _{1}(t)$ વડે તથા સમાન સમય અંતરાલ પછી બીજા પદાર્થનું સ્થાન $x _{2}(t)$ વડે અપાય છે. નીચેનામાંથી ક્યો આલેખ $\left( x _{1}- x _{2}\right)$ ને સમય $t$ ના વિધેય તરીકે સાચી રીતે દર્શાવે છે?View Solution
- 7એક $120 \,m$ લાંબી ટ્રેન પશ્ચિમ તરફ $10\, m/s$ ની ઝડપે ગતિ કરે છે. એક પક્ષી પૂર્વ તરફ $5\, m/s$ ની ઝડપથી ટ્રેન ને પસાર કરે છે. તો ટ્રેન પસાર કરવા માટે પક્ષીને કેટલા .........$sec$ નો સમય લાગશે?View Solution
- 8A body falling under gravity covers two points $\mathrm{A}$ and $\mathrm{B}$ separated by $80 \mathrm{~m}$ in $2 \mathrm{~s}$. The distance of upper point A from the starting point is $\mathrm{m}$ (use $\mathrm{g}=10 \mathrm{~ms}^{-2}$ ).View Solution
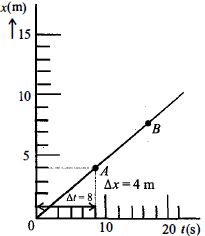
- 9કોઈ પદાર્થની ગતિનો આલેખ આકૃતિમાં દર્શાવેલો છે. બિંદુઓ $A$ અને $B$ પાસે તેનો તત્કાલિન વેગ અનુક્રમે $v_A$ અને $v_B$ છે. તો$.........$View Solution
- 10એક હેલિકોપ્ટર સ્થિર સ્થિતિમાંથી શિરોલંબ ઉપર તરફ અચળ પ્રવેગ $g$ થી ગતિ કરે છે. જ્યારે હેલિકોપ્ટરની ઊંચાઈ $h$ થાય, ત્યારે તેમાંથી એક ફૂડ પેકેટને મુક્ત કરવામાં આવે છે. ફૂડ પેકેટને જમીન પર પહોચવા માટે લાગતો સમય લગભગ કેટલો હશે? $[g$ ગુરુત્વપ્રવેગ છે]View Solution