$x-$અક્ષ પર ગતિ કરતા કણનું સ્થાન $x = 9{t^2} - {t^3}$ મુજબ આપવામાં આવે છે. જયાં $ x$ મીટરમાં અને $t$ સેકન્ડમાં છે. જયારે કણ ધન $x-$ દિશામાં મહત્તમ ઝડપ પ્રાપ્ત કરે ત્યારે ત્યારે $+x$ દિશામાં કણનું સ્થાન $(m$ માં$)$ શું હશે?
AIPMT 2007, Medium
Download our app for free and get started
Give : $x=9 t^2-t^3$
Speed $v=\frac{d x}{d t}=\frac{d}{d t}\left(9 t^2-t^3\right)=18 t-3 t^2$.
For maximum speed, $\frac{d v}{d t}=0$
$\Rightarrow 18-6 t=0$
$\therefore t=3 s$.
$\therefore x_{\text {max }}=81 m-27 m=54 m. ($From $\left.x=9 t^2-t^3\right)$
Speed $v=\frac{d x}{d t}=\frac{d}{d t}\left(9 t^2-t^3\right)=18 t-3 t^2$.
For maximum speed, $\frac{d v}{d t}=0$
$\Rightarrow 18-6 t=0$
$\therefore t=3 s$.
$\therefore x_{\text {max }}=81 m-27 m=54 m. ($From $\left.x=9 t^2-t^3\right)$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રારંભમાં વિરામ સ્થાને થી $x$-અક્ષ સાથે $x=0$ આગળના સંદર્ભ બિંદુ થી $v$ વેગ થી કે જે $v=4 \sqrt{x} \mathrm{~m} / \mathrm{s}$ મુજબ બદલાય છે. તે રીતે ગતિ કરવાનું શરૂ કરે છે. કણનો પ્રવેગ_____$\mathrm{ms}^{-2}$હશે.View Solution
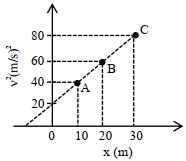
- 2એક કણ અચળ પ્રવેગ $a$ થી ગતિ કરે છે. તેનો $v^{2}$ વિરુદ્ધ $x$ (સ્થાનાંતર) નો ગ્રાફ આપેલ છે. કણનો પ્રવેગ (${m} / {s}^{2}$ માં) કેટલો હશે?View Solution
- 3નીચેનામાંથી કયો સ્થાનતર $(X)$ નો સમય સાથેનો ગ્રાફ શક્ય નથી?View Solution
- 4એક પદાર્થ સ્થિર સ્થિતિમાંથી અચળ પ્રવેગથી $10 \,sec$ માં $27.5\, m/s$ નો વેગ પ્રાપ્ત કરે છે.તો તેની પછીની $10 \,sec$ માં તેણે કેટલા.........$m$ અંતર કાપ્યું હશે?View Solution
- 5View Solutionમુક્ત પતન કરતા એક પદાર્થ ના પ્રથમ,દ્રિતીય,તૃતીય અને ચોથી સેકન્ડમાં કપાયેલ અંતરોનો ગુણોતર ......... હોય છે.
- 6એક કાર $150\,km/h$ ની ઝડપથી ગતિ કરે છે અને બ્રેક લગાવ્યા બાદ તે $27\,m$ અંતર કાપીને તે અટકે (સ્થિર) છે. જો આ જ કારે નોંધેલ ઝડ૫ કરતા એક તૃતિયાંશ ઝડપે ગતિ કરતી હોય, તો તે કેટલું અંતર ($m$ માં) કાપીને સ્થિર થશે?View Solution
- 7$60 \,km/h$ ઝડપે ગતિ કરતા વાહનને બ્રેક લગાવ્યા બાદ તે $20\, m$ જેટલું અંતર કાપીને ઊભું રહે છે.આ વાહન બમણી ઝડપથી (એટલે કે $120 \,km/h$ થી ) ગતિ કરતું હોય, તો વાહનનું સ્ટોપિંગ ડિસ્ટન્સ ($m$ માં) કેટલું થાય?View Solution
- 8એક કણ $4 \,m$ લંબાઇની નળીમાં $1\, km/sec$ ની ઝડપથી દાખલ થાય છે,અને $9 \,km/sec$ ની ઝડપથી બહાર આવે છે,તો તે નળીમાં કેટલા સમય સુધી રહ્યો હશે?View Solution
- 9એક ગ્રહ પર બોલને $100\; m$ ઊંચાઈના ટાવર પરથી મુક્ત કરવામાં આવે છે. જમીન પર પહોચતા પહેલા છેલ્લી $\frac{1}{2}\;s $ માં તે $19\; m$ અંતર કાપે છે. ગ્રહની સપાટી નજીક ગુરુત્વ પ્રવેગનું મૂલ્ય (${ms}^{-2}$ માં) કેટલું હશે?View Solution
- 10View Solutionવિધાન: મુક્તપતન માં પદાર્થ નું વજન અસરકારક રીતે શૂન્ય જણાય છે.
કારણ: મુક્તપતન કરતાં પદાર્થ માટે ગુરુત્વપ્રવેગ શૂન્ય હોય.