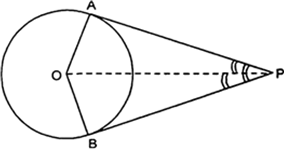
यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80º के कोण पर झुकी हों, तो $\angle$POA बराबर है:
Exercise-10.2-3
Download our app for free and get started
$\triangle$POA और $\triangle$POB में,
PA = PB (बाह्य बिंदु से समान स्पर्श रेखाएँ)
OA = OB (वृत्त की त्रिज्याएँ)
और OP = OP (उभयनिष्ठ)
$\therefore \triangle$POA $\cong \triangle$POB (SSS सर्वांगसमता)
$\Rightarrow \angle$OPA = $\angle$OPB
$\Rightarrow \angle$OPA = $\angle$OPB = $\frac{1}{2} \times$ 80º = 40º
हम जानते हैं कि वृत्त की त्रिज्या और स्पर्श रेखा के बीच 90º का कोण होता है।
$\therefore \angle$OAP = 90º
अब $\triangle$ОAP में,
$\angle$OAP + $\angle$OPA + $\angle$POA = 180º
$\Rightarrow$ 90º + 40º + $\angle$POA = 180º
$\Rightarrow$ 130º + $\angle$POA = 180º
$\Rightarrow \angle$POA = 50º
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solution
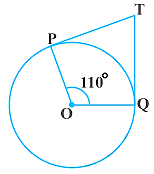
आकृति में, यदि TP, TQ केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि $\angle$POQ = 110°, तो $\angle$PTQ बराबर है:
- 2View Solutionसिद्ध कीजिए कि दो सकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है।
- 3एक बिंदु $Q$ से एक वृत्त पर स्पर्श रेखा की लंबाई $24 \ cm$ तथा $Q$ की केंद्र से दूरी $25 \ cm$ है। वृत्त की त्रिज्या है:View Solution
- 4केंद्र $O$ वाले वृत्त पर बाह्य बिंदु $T$ से दो स्पर्श रेखाएँ $TP$ तथा $TQ$ खींची गई हैं। सिद्ध कीजिए कि $\angle \text{PTQ} = 2 \angle \text{OPQ}$ है।View Solution
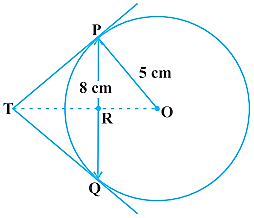
- 5$5 \ cm$ त्रिज्या के एक वृत्त की $8 \ cm$ लंबी एक जीवा $PQ$ है। $P$ और $Q$ पर स्पर्श रेखाएँ परस्पर एक बिंदु $T$ पर प्रतिच्छेद करती हैं $($देखिए आकृति$)$। $TP$ की लंबाई ज्ञात कीजिए।View Solution
