યંગના ડબલ -સ્લિટના પ્રયોગમાં બંને સ્લિટ એકબીજાથી $2\; mm$ દૂર છે અને તે $\lambda_1= 12000\;\mathring A$ અને $ \lambda_2= 10000\;\mathring A$ એમ બે તરંગલંબાઇવાળા ફોટોન્સથી પ્રકાશિત કરવામાં આવે છે. સ્લિટથી $ 2\; m$ અંતરે રહેલા પડદા પર સામાન્ય મઘ્યસ્થ પ્રકાશિત શલાકાથી કયા લઘુતમ અંતર ($mm$ માં) માટે એક વ્યતિકરણ ભાતની પ્રકાશિત શલાકા અને બીજા પ્રકાશિત શલાકા એકબીજા પર સંપાત થશે?
AIPMT 2013, Diffcult
a
Let \(n_{1}\) bright fringe of \(\lambda_{1}\) coincides with \(n_{2}\) bright fringe of \(\lambda_{2}\). Then
Let \(n_{1}\) bright fringe of \(\lambda_{1}\) coincides with \(n_{2}\) bright fringe of \(\lambda_{2}\). Then
\(\frac{{{n_1}{\lambda _1}D}}{d} = \frac{{{n_2}{\lambda _2}D}}{d}\) or \({n_1}{\lambda _1} = {n_2}{\lambda _2}\)
\(\frac{{{n_1}}}{{{n_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{10000}}{{12000}} = \frac{5}{6}\)
Let \(x\) be given distance.
\(\therefore \quad x=\frac{n_{1} \lambda_{1} D}{d}\)
Here, \({n_1} = 5,\) \(D = 2\,{\text{m}},\) \(d = 2\,{\text{mm}}\) \( = 2 \times {10^{ - 3}}{\text{m}}\)
\({\lambda _1} = 12000\,\mathop {\text{A}}\limits^o \) \( = 12000 \times {10^{ - 10}}{\text{m}}\) \( = 12 \times {10^{ - 7}}{\text{m}}\)
\(x = \frac{{5 \times 12 \times {{10}^{ - 7}}{\text{m}} \times 2{\text{m}}}}{{2 \times {{10}^{ - 3}}{\text{m}}}}\) \( = 6 \times {10^{ - 3}}{\text{m}} = 6\,\,{\text{mm}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$A $ પહોળાઈ ધરાવતી સ્લિટ, એકરંગીય પ્રકાશ દ્વારા પ્રકાશિત કરવામાં આવે છે. જેની તરંગલંબાઈ $650$ નેનોમીટર $ (nm)$ છે. જ્યારે પ્રથમ ન્યૂનત્તમ એ $30$ વિવર્તનકોણે રચાય ત્યારે સ્લિટની પહોળાઇ .....હશે .View Solution
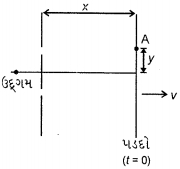
- 2યંગના બે સ્લિટના પ્રયોગમા પડદો $v$ જેટલી અચળ ઝડપે જમણી બાજુ ખસે છે. સ્લિટના સમતલ અને પડદા વચ્ચે શરૂઆતનુ અંતર $x$ છે. $t=0$ સમયે પહેલા ક્રમનુ મહતમ બિંદુ $A$ પાસે છે. કેટલા સમય પછી બિંદુ $A$ પાસે પ્રથમ ક્રમનુ લઘુતમ હશે.View Solution
- 3યંગના ડબલ સ્લિટના પ્રયોગમાં એક સ્લિટના માર્ગમાં જાડાઇ $2.5 \times 10^{-5} m$ અને $ (\mu = 1.5) $ વક્રીભવનાંક ધરાવતી તકતી મૂકતાં મધ્યમાન પ્રકાશિત શલાકા કેટલા ....$cm$ અંતર ખસે? બે સ્લિટ વચ્ચેનું અંતર $0.5mm$ અને સ્લિટ અને પડદા વચ્ચેનું અંતર $100 cm$ છે.View Solution
- 4એક સ્લિટની પહોળાઈ $a$ પર $5000 \;\mathring A$ તરંગલંબાઈનો પ્રકાશ આપાત કરવામાં આવે, ત્યારે મળતા વિવર્તનમાં $ 30^o $ ના ખૂણે પ્રથમ ન્યુનતમ મળે છે. પ્રથમ ગૌણ મહત્તમ કેટલા કોણે દેખાશે?View Solution
- 5યંગના બે સ્લીટના પ્રયોગમાં, સ્લીટો વચ્ચેનું અંતર $0.5$ $mm$ છે અને સ્ક્રીનને $150$ $cm $ દૂર રાખેલ છે. $650$ $nm$ અને $520$ $nm$ એમ બે તરંગલંબાઇ ધરાવતો પ્રકાશપુંજ પડદા પર વ્યતિકરણ મેળવવા માટે ઉપયોગમાં લેવાય છે.કોમન સેન્ટ્રલ મહત્તમથી જયાં બંને તરંગલંબાઇઓ દ્વારા રચાતી તેજસ્વી શલાકાઓ સંપાત થાય છે,તેનું લઘુત્તમ અંતર .......$ mm$ છે.View Solution
- 6બે તરંગો માંથી પ્રત્યેકની તીવ્રતા $ I$ હોય, અને તેઓ વચ્ચે $120^o$ નો કળા તફાવત હોય તો ત્યારે તરંગો સંપાત થશે તો તેમની પરિણામી તીવ્રતા ......View Solution
- 7યંગના દ્વિ સ્લીટ પ્રયોગમાં બે સ્લીટો વચ્ચેનું વિયોજન $3 \,mm $ છે અને $480 \,nm$ તરંગલંબાઈવાળા પ્રકાશથી પ્રકાશિત કરવામાં આવે છે. સ્લીટોના સમતલથી પડદો $2\, m$ અંતરે છે. કેન્દ્રિય પ્રકાશિત શલાકાના સંદર્ભમાં $8$ મી પ્રકાશિત શલાકા અને $3$ જી અપ્રકાશિત શલાકા વચ્ચેનું વિયોજન શોધો.View Solution
- 8View Solutionપ્રકાશનો તરંગ સ્વભાવ કઇ ઘટનાથી મળે છે?
- 9View Solutionવ્યતિકરણ માટે કેવા ઉદ્ગમની જરૂર પડે?
- 10કાચના સ્લૅબ પર $57.5^{0}$ જેટલા ધ્રૂવીભૂતકોણે અધ્રુવીભૂત પ્રકાશ આપાત કરવામાં આવે છે, તો આપાતકિરણ અને વક્રીભૂત કિરણ વચ્ચેનો ખૂણો .......$^o$ હશે.View Solution
