યંગના ડબલ સ્લિટના પ્રયોગમાં એક સ્લિટના માર્ગમાં $t$ જાડાઇ અને $\mu$ વક્રીભવનાંક ધરાવતી તકતી મૂકતાં બે કિરણો વચ્ચે પથ તફાવત કેટલો થાય?
Easy
Download our app for free and get started
b
(b) Change in the optical path \(=\mu t-t\)
(b) Change in the optical path \(=\mu t-t\)
\(=(\mu-1) t\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકૃતિમાં દ્વિ સ્લીટ પ્રયોગ બતાવ્યો છે. દરેક સ્લીટની પહોળાઈ $ W$ છે. એક જાડાઈનો, $\mu$ વક્રીભવનાંકવાળો પાતળો ગ્લાસનો ટુકડો સ્લીટ અને પડદાની વચ્ચે મુકવામાં આવે છે. કેન્દ્રીય બિંદુએ તીવ્રતા જાડાઈ ના વિધેય તરીકે માપવામાં આવે છે. જાડાઈ ની કઈ કિંમતે $C$ પર તીવ્રતા ન્યૂનત્તમ હશે?View Solution
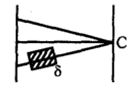
- 2View Solutionદ્રવ્યનો વક્રીભવનાંક એ ધ્રુવીભુત કોણના બરાબર હોય છે. તેને .....
- 3યંગના બે સ્લીટના પ્રયોગમાં $800\,nm$ તરંગલંબાઇનો પ્રકાશ બંને સ્લીટ પર આપાત કરવામાં આવે છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે $A _1 A _2$ ને જોડતી રેખા $A _1 P$ લંબ છે. જો બિંદુ $P$ આગળ ન્યૂનતમ રયાય તો સ્લીટ વચ્ચેનું અંતર $.......\,mm$ થાય.View Solution
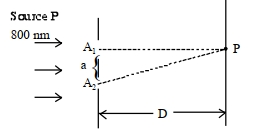
- 4View Solutionબે સમાન પાવર ધરાવતા સોડિયમ લેમ્પમાં વ્યતિકરણની ઘટના અવલોકી શકાતી નથી કારણ કે બન્ને તરંગોને .....
- 5$Io$ તીવ્રતા ઘરાવતા અધ્રુવીભૂત પ્રકાશ કિરણપુંજ $(beam)$ ને પોલેરોઇડ $A $ અને ત્યારબાદ બીજા પોલેરોઇડ $B$ નું મુખ્ય સમતલ પોલેરોઇડ $A$ ની સાપેક્ષ $45°$ નો કોણ બનાવતું હોય,તો નિર્ગમન પામતા પ્રકાશની તીવ્રતા ______ થશે.View Solution
- 6View Solutionફ્રોનહોફર વિર્વતનમાં સ્લિટ પર આપાત થતાં તરંગઅગ્રનો આકાર કેવો થાય?
- 7યગ્રનાં ડબલ સ્લીટ પ્રયોગ માં એલ સ્લીટ બીજી કરતા વધારે પહોળી છે કે જેથી પહેલી સ્લીટમાંથી નીકળતા પ્રકાશને કંપ વિસ્તાર બીજીમાંથી નીકળતા પ્રકાશનાં કંપ વિસ્તાર કરતાં બમણો છે. જો $I_m$ મહત્તમ તિવ્રતા હોય તો જ્યારે તેઓ $\phi$ કળા તફાવતે વ્યતિકરણ પામે ત્યારે પરીણામી તિવ્રતા .............. વડે દર્શાવાય છે.View Solution
- 8$\lambda-7000\; \mathring A$ ના પ્રકાશ માટે, યંગના ડબલ સ્લિટ પ્રયોગમાં $Interference $ પેટર્નમાં એક બિંદુ આગળ $10$ મી ક્રમની અધિકતમ રચાય છે, જો તરંગલંબાઈ $\lambda=5000\; \mathring A$ કરવામાં આવે તો તે જ બિંદુ આગળ અધિકતમ $...........$View Solution
- 9બે સુસંબદ્ધ સ્ત્રોતોની મદદથી મેળવાયેલી વ્યતિકરણ ભાતમાં તીવ્રતાનો ફેરફાર એ સરેરાશ તીવ્રતાના $5\%$ જેટલો છે. તે બે સ્ત્રોતોની તીવ્રતાનો ગુણોત્તર શોધો.View Solution
- 10View Solutionગૌણ તરંગો માટે હાઈગેનનો સિદ્ધાંત .......શોધવા ઉપયોગમાં લઈ શકાય.