Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1હાઇડ્રોકાર્બન હાઇપોક્લોરસ એસિડ સાથે પ્રક્રિયા કરી $1-$ ક્લોરો $-2-$ હાઇડ્રોક્સિઇથેન આપે છે ,એ કયો હાઇડ્રોકાર્બન છે?View Solution
- 2View Solutionઘન મિથેન એ .....
- 3View Solutionઓછા કાર્બન નંબરના હાઇડ્રોકાર્બન તૈયાર કરવાની સૌથી મહત્વપૂર્ણ પદ્ધતિ કઈ છે?
- 4જ્યારે નિર્જળ $AlC{l_3}$ની હાજરીમાં ${C_6}{H_6}$ ની વધારે માત્રા $C{H_2}C{l_2}$ સાથે પ્રક્રિયા કરે છે તો નીચેનામાંથી ક્યુ બંધારણ અપેક્ષિત નીપજને અનુરૂપ છેView Solution
- 5View Solutionકાર્બન-કાર્બન બંધ લંબાઈ ઓછામાં ઓછી કોનામાં છે?
- 6$CH _{3}- C \equiv CH \stackrel{2 HBr }{\longrightarrow} \stackrel{ H _{2} O }{\longrightarrow}$ નીપજ, નીપજ કઈ છે:View Solution
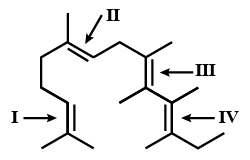
- 7નીચેની કોની રચનામાં, $I$, $II$, $III$ અને $IV$ દ્વિબંધ ચિહ્નિત થયેલ છે?View Solution
- 8View Solutionનીચેનામાંથી કોણ વુર્ટઝ-ફીટિગ પ્રક્રિયા રજૂ કરે છે?
- 9નીચેની પ્રક્રિયા ક્રમમાં છેલ્લી નીપજ $(C)$ કઈ હશે?View Solution
$HC\, \equiv \,CH\,\xrightarrow[{20\% \,{H_2}S{O_4}}]{{1\% \,HgS{O_4}}}A$ $\xrightarrow[{{H_2}O}]{{C{H_3}MgX}}B\xrightarrow{{[O]}}(C)$
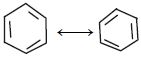
- 10વિધાન : બેન્ઝિન$C -C$ એકલ બંધ અને $C = C$ દ્વિબંધને કારણે બે જુદી જુદી બંધ લંબાઈ દર્શાવે છે.View Solution
કારણ : બેન્ઝિનની વાસ્તવિક રચના એ નીચેના બે બંધારણોનો એક વર્ણસંકર છે.
- 11નીચે આપેલ પ્રક્રિયામાં $X$ એ શું હશે?View Solution
$C{H_3}C{H_2}CH = CHC{H_3}$ $\xrightarrow{X}C{H_3}C{H_2}COOH\, + \,C{H_3}COOH$
- 12View Solutionસૌથી મજબૂત ઓર્થો - પેરા અને સૌથી મજબૂત મેટા - જૂથો અનુક્રમે છે....
- 13કયો આલ્કીન જે $HBr$ની ગેરહાજરીમાં તેમજ પેરોક્સાઇડની હાજરીમાં સમાન નીપજ આપશે ....View Solution
- 14નીચેનામાંથી સંયોજનને $(3)$ બાકીના સંયોજનોમાંથીઅલગ પાડવા માટે કયો સૌથી યોગ્ય પ્રક્રિયક છે ?View Solution
$1.\,\,CH_3-C \equiv C -CH_3$
$2.\,\,CH_3 - CH_2 - CH_2 - CH_3$
$3. \,\,CH_3 - CH_2C \equiv CH$
$4.\,\,CH_3 - CH = CH_2$
- 15નીચેનામાંથી કઈ પ્રક્રિયા ફ્રીડલ-ક્રાફ્ટ્ આલ્કાઈલેશન પ્રક્રિયામાં મુખ્ય નીપજ તરીકે $2-$ફિનાઇલબ્યુટેન આપશે નહીં ?View Solution
- 16નીચની પ્રક્રિયામાં $P$ શોધો.View Solution
$C{H_3}C \equiv \,CC{H_3}\,\xrightarrow[{{\text{heat}}}]{{NaN{H_2}/{\text{inert solvent}}}}P$
- 17View Solutionનીચે પૈકી કયું ઓછી દ્વિધ્રુવીય ચાકમાત્રા ધરાવે છે?
- 18View Solutionપોલિવિનાઇલ આલ્કોહોલ કોની દ્વારા બનાવી શકાય છે ?
- 19આપેલા વિધાનો ધ્યાનમાં લો :View Solution
હાઈડ્રોકાર્બન જેની આણ્વિય રચના $C_5H_{10}$ છે
$I.$ એકલવિસ્થાપનીય આલ્કિન
$II.$ દ્વિવિસ્થાપનીય આલ્કિન
$III.$ ત્રિવિસ્થાપનીય આલ્કિન
નીચે પૈકી ક્યાં વિધાન/વિધાનો સાચા છે?
- 20View Solutionનીચેનામાંથી કયું એક વુર્ટ્ઝ પ્રક્રિયા દ્વારા તૈયાર કરી શકાતું નથી?
- 21View Solutionરાસાયણિક પદ્ધતિ અનુસાર બિન-ચક્રીય છે,...
- 22$1-$ બ્યુટિનને $2-$ બ્યુટિન દ્વારા ખૂબ સરળતાથી ઓળખી શકાય છેView Solution
- 23સંયોજન $X$નું પરમાણ્વીય સૂત્ર $C_4H_6$ $Pt$ ની હાજરીમાં હાઈડ્રોજન જેવુ એક સમકક્ષ બીજું સંયોજન $Y$ બનાવે છે, જે ઓઝોનોલિસીસ પર ફક્ત ઇથેનોઇક એસિડ આપે છે. સંયોજન $X$ હોઈ શકે છેView Solution
- 24$(CH_3)_2C = CHCH_3 + NOBr \to $ નીપજ. નીપજનું બંધારણ શું છે?View Solution
- 25View Solutionનીચા કાર્બન નંબરના હાઇડ્રોકાર્બન તૈયાર કરવાની સૌથી મહત્વપૂર્ણ પદ્ધતિ કઈ છે
- 26View Solutionનીચેનો કયો ઘટક બેન્ઝિન રિંગના સલ્ફોનેશનમાં ભાગ લે છે?
- 27View Solutionમર્ક્યુરેશન અને ડીમર્ક્યુરેશન ઉત્પન્ન કરે છે,....
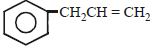
- 28$C_6H_5CH_2CH_3$ ને $C_6H_5CH = CH_2$ માં રૂપાંતર માટે નીચેના પ્રક્રિયાઓ (પ્રક્રિયકો) નો કયો ક્રમ વાપરી શકાય છે?View Solution
- 29View Solutionનીચે, કેટલાક ઉદ્વીપક અને અનુરૂપ પ્રક્રિયા / પ્રક્રિયાઓ સમાન થાય છે. અસમાન છે,...
- 30$HBr$ની પ્રક્રિયા $3-$ફિનાઇલપ્રોપીન પર કરતાં.... (મુખ્ય નીપજ તરીકે)View Solution
- 31View Solutionપિરીડીન એ ટ્રાઇથાઇલએમાઇન કરતા ઓછું બેઝિક છે કારણ કે
- 32નીચેની પ્રકિયા ની મુખ્ય નીપજ કઈ છે ?View Solution
$\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{\,\,\,\,\,\,\,C{H_3}} \\
|
\end{array}} \\
{C{H_3} - C - C{H_3}} \\
| \\
H
\end{array}{\mkern 1mu} $ $\mathop {\xrightarrow{{C{H_3}OBr}}}\limits_{C{H_3}OH} $ - 33View Solutionનિચે પૈકી કયો એરોમેટિક સંયોજન ધરાવે છે?
- 34જ્યારે એસિટિલિન મંદ સલ્ફ્યુરિક એસિડમાં પસાર થાય છે જેમાં $H{g^{2 + }}$ આયન હોય છે, ત્યારે બનાવેલ નીપજView Solution
- 35View Solutionનીચે પૈકી કોણ મહત્તમ સ્થાયીતા ધરાવે છે?
- 36$C{H_2} = CH - {(C{H_2})_2}COOH$ને પેરોક્સાઇડની હાજરીમાં $HBr$ સાથે પ્રક્રિયા આપે ત્યારે નીચેનામાંથી કયું સંયોજન ઉત્પન્ન થાય છે?View Solution
- 37View Solutionજો ઇથિલિન, કાર્બન મોનોક્સાઇડ અને પાણીને ઊંચા તાપમાને ગરમ કરવામાં આવે તો નીચેનામાંથી કયું રચાય છે?
- 38${C_6}{H_6}\mathop {\xrightarrow{{HN{O_3}}}}\limits_{{H_2}S{O_4}} X\mathop {\xrightarrow{{C{l_2}}}}\limits_{FeC{l_3}} Y$.અહીંયા $Y$ એ શું છે?View Solution
- 39View Solutionઆલ્કીન સામાન્ય રીતે કઈ પ્રકારની પ્રક્રિયા આપે છે?
- 40પ્રોપીન $HBr$ સાથે પ્રક્રિયા કરીને શું આપે છે?View Solution
- 41View Solutionબેન્ઝીનને જ્યારે સૂર્યપ્રકાશની હાજરીમાં ક્લોરિન સાથે ગરમ કરવામાં આવે છે ત્યારે શું રચાય છે?
- 42શાખિત સાંકળ વાળા આલ્કેન્સનો $B.P.$ સીધી સાંકળ વાળા આલ્કેન્સની સરખામણીમાં .... છે.View Solution
- 43View Solutionનીચે પૈકી કયું સૌથી સ્થાયી આલ્કીન છે?
- 44${C_6}{H_6} + C{H_3}Cl\mathop {\xrightarrow{{{\text{anhydrous}}}}}\limits_{AlC{l_3}} {C_6}{H_5}C{H_3} + HCl$View Solution
ઉપરની પ્રક્રિયા કોનું ઉદાહરણ છે?
- 45View Solutionબેયરની પ્રક્રિયકનો પ્રયોગશાળામાં ઉપયોગ શું થાય છે?
- 46$1-$ બ્યુટાઇન ઠંડા આલ્કલાઇન $KMn {O_4}$ સાથેની પ્રક્રિયાથી શું આપે છેView Solution
- 47કેલ્શિયમ કાર્બાઇડમાંથી પોલિઇથિલિનની રચના નીચે મુજબ થાય છેView Solution
$Ca{C_2} + 2{H_2}O \to Ca{(OH)_2} + {C_2}{H_2}$
${C_2}{H_2} + {H_2} \to {C_2}{H_4}$
$n({C_2}{H_4}) \to {( - C{H_2} - C{H_2} - )_n}$
$64.1\, kg$ $Ca{C_2}$માંથી મેળવેલ પોલિઇથિલિનનો જથ્થો ......$kg$ છે.
- 48View Solutionનીચેનામાંથી કયું વિધાન ઇથેન માટે સાચું નથી?
- 49View Solutionપેટ્રોલિયમ રિફાઇનિંગ શું છે?
- 50View Solutionબેન્ઝીનનું ઉદીપકીય હાઇડ્રોજનીકરણ શું આપે છે?
- 51View Solutionસોડિયમ બેન્ઝોએટ અને સોડાલાઇમના મિશ્રણને ગરમ કરવા પર, નીચે પૈકી શું પ્રાપ્ત થાય છે?
- 52View Solutionનીચેનામાંથી કયું મોનોક્લોરિનેશન પર મેટા વિસ્થાપનમાંથી પસાર થશે
- 53View Solutionનીચે પૈકી કોના દ્વારા ઓલિફીન્સને હાઇડ્રોજનિત કરી શકાય છે?
- 54$\begin{array}{*{20}{c}}View Solution
{CH} \\
{|||\,\,\,\,\,} \\
{CH}
\end{array}$ $\xrightarrow{{{O_3}/NaOH}}X\xrightarrow{{Zn/C{H_3}COOH}}Y$ ‘$Y$’ શું છે? - 55'$ X $' સંયોજનના ઓઝોનીકરણ પર $HCHO$ના બે પરમાણુ બને છે. સંયોજન '$X$' શું હશે?View Solution
- 56View Solutionનીચે પૈકી કયો બંધ ધરાવતો હાઇડ્રોકાર્બન સૌથી વધુ ક્રિયાશીલ છે?
- 57View Solutionશું થાય છે જ્યારે એસિટિલિન અને હાઇડ્રોજનનું મિશ્રણને ગરમ લિન્ડલરના ઉદીપક પરથી પસાર કરવામાં આવે છે.
- 58સૂર્યપ્રકાશમાં $C{H_4}$ની $C{l_2}$ની પ્રક્રિયા દ્વારા નીચે પૈકી કયુ બનતું નથી?View Solution
- 59$C{H_3} - CH = C{H_2} + HBr\xrightarrow{{}}..........,$ ઉત્પન્ન થતી નીપજ કઈ હશે?View Solution
- 60નીચે આપેલી પ્રક્રિયામાં $C{H_3} - C{H_2} - C{H_2} - C{H_3} \xrightarrow[475\, K]{H_2SO_4}$View Solution
- 61નીચેની શૃંખલામાં $Z$ શું હશે?View Solution
$C{H_2} = C{H_2}\xrightarrow{{HBr}}X\xrightarrow{{{\text{Hydrolysis}}}}Y\mathop {\xrightarrow{{N{a_2}C{O_3}}}}\limits_{{I_2}{\text{ excess}}} Z$
- 62$72\,u$ આણ્વિય દળ ધરાવતા હાઇડ્રોકાર્બનનો ક્યો શાખીય શૃંખલાવાળો સમઘટક એક વિસ્થાપિત આલ્કાઇલ હેલાઇડનો ફક્ત એક જ સમઘટક આપે ?View Solution
- 63$2-$ હેકઝાઇનની કોની સાથેની પ્રક્રિયાથી ટ્રાન્સ$-2-$હેકિઝન મળે?View Solution
- 64ઇથાઈલ બેન્ઝિન અને $N-$બ્રોમોસકસીનીએમાઇડ ની પ્રક્રિયાથી નીપજ મળશે?View Solution
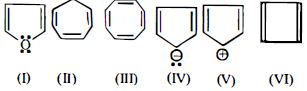
- 65View Solutionનીચે પૈકી કયા સંયોજન બિન-ચક્રીય છે?
- 66સૂર્યપ્રકાશની હાજરીમાં $2-$મિથાઇલ બ્યુટેનની બ્રોમીન સાથેની પ્રક્રિયાથી મુખ્યત્વે ...મળે છે.View Solution
- 67View Solutionએક કાર્બનિક પદાર્થના ઓઝોનોલિસીસથી એક નીપજ ફોર્માલ્ડિહાઇડ મળે છે. જે તેમાં શાની હાજરી પૂરવાર કરે છે ?
- 68એક મોલ સમમિતિય આલ્કિનના ઓઝોનોલિસીસથી $44\, u.$ અણુભારવાળા આલ્ડિહાઇડના બે મોલ મળે તો તે આલ્કીન ક્યો હશે ?View Solution
- 69$CH_3C \equiv C-H$ ની $CH_3MgX$ સાથેની પ્રક્રિયાથી શું મળે ?View Solution
- 70View Solutionટોલ્યુઇન નાઇટ્રેટ થાય છે અને ટીન અને હાઇડ્રોક્લોરિક એસિડથી પરિણામી નીપજ ઓછી થાય છે.આથી પ્રાપ્ત થયેલ નીપજ ડાયઝોટાઇઝ્ડ છે અને પછી ક્યુપ્રસ બ્રોમાઇડ સાથે ગરમ થાય છે. પ્રક્રિયા મિશ્રણ ધરાવે છે.......
- 71નીચેની પ્રક્રિયા શ્રેણીમાં આલ્કીન એ સંયોજન $B$ આપે છે. તો સંયોજન $B$ ...... થશે.View Solution
$CH_3 - CH = CH - CH_3 \xrightarrow{{{O_3}}} A $$\xrightarrow[{Zn}]{{{H_2}O}} B.$
- 72View Solutionહાઇડ્રોકાર્બન કે જે સોડિયમ સાથે પ્રવાહી એમોનિયામાં પ્રક્રિયા કરે .............
- 73$FeCl_3$ ની હાજરીમાં ટોલ્યુઇનની ક્લોરિન સાથેની પ્રક્રિયાથી મુખ્યત્વે ...... મળે છે.View Solution
- 74$KMnO_4$ દ્વારા ઇથાઇલ બેન્ઝિનના ઓક્સિડેશનના પરિણામે રચિત સંયોજન છેView Solution
- 75નીચેનામાંથી કઇ પ્રક્રિયા $2,2-$ડાયબ્રોમો પ્રોપેન આપશે ?View Solution
- 76${40\,^o}C$ પર $1,3-$બ્યુટાડાઈનના એક અણુ સાથે $HBr$ના એક અણુની પ્રક્રિયા મુખ્યત્વે આપે છેView Solution
- 77View Solutionનીચેનામાંથી સૌથી વધારે બેઝિક સંયોજન છે...
- 78View Solutionપાંચ સમઘટકીય હેકઝેનમાંથી બે મોનોક્લોરો વ્યુત્પન્ન આપતું સંયોજન . ... છે.
- 79સૂર્યપ્રકાશની હાજરીમાં $2-$મિથાઇલ બ્યુટેનની બ્રોમીન સાથેની પ્રક્રિયાથી મુખ્યત્વે ...... મળે છેView Solution
- 80View Solutionઆમાંના કયા પ્રતિ-માર્કોનિકોવના નિયમનું પાલન કરતા નથી
- 81View Solutionચોક્કસ આલ્કેનની પારજાંબલી પ્રકાશની હાજરીમાં પ્રક્રિયા કરતા ફક્ત એક જ મોનોક્લોરો વ્યુત્પન્ન મળે છે. તો તે આલ્કેન ........... હોય.
- 82બ્યુટીન$-1$ નું બ્યુટેનમાં રૂપાંતર ... સાથેની પ્રક્રિયાથી થાય છે.View Solution
- 83View Solutionએસિટિલિનની હાઇપોક્લોરસ એસિડ સાથેની પ્રક્રિયાથી મળતી નીપજ કઇ છે ?
- 84View Solutionનીચેનામાંથી કોણ એસિટિલિન સાથે પ્રક્રિયા કરશે નહિ ?
- 85${(C{H_3})_2}C = CH - C{H_2}C{H_2}C{H_3}$નું પરમેંગેનેટ દ્રાવણ દ્વારા ઝડપી ઓક્સિડેશન કરતાં શું આપે છેView Solution
- 86$0.72$ ગ્રામ પાણી અને $3.08$ ગ્રામ $CO_2$ ના દહનથી હાઈડ્રોકાર્બન વાયુ મળે છે તો આ હાઈડ્રોકાર્બન વાયનું મોલ પ્રમાણ સૂત્ર કયું થાય ?View Solution
- 87View Solutionઆપેલી પ્રકિયા માં મળતી મુખ્ય નીપજ કઈ છે ?
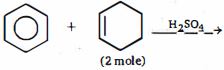
- 88View Solutionઉપરોક્ત રૂપાંતર કરવા માટે.પ્રકીયક ને ઘટતો ક્રમ કયો છે ?
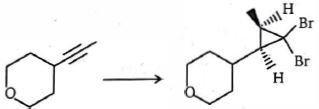
- 89View Solutionનીચેનામાંથી કયા સંયોજન સૌથી સ્થાયી છે
- 90નીચે બતાવેલ તબબકું એ કોરેન્યુલિનનું તાજેતરનું સંશ્લેષણ છે.View Solution
નીપજ $(A)$ શું હશે ?
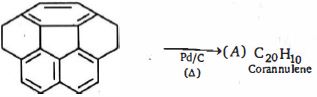
- 91નીપજ $(A)$ શું હશે ?View Solution
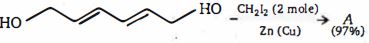
- 92નીપજ $(B)$ શું હશે ?View Solution

- 93નીપજ $Y$ શું હશે ?View Solution
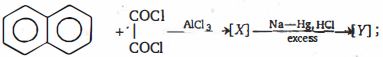
- 94View Solutionપ્રકિયા ની મુખ્ય નીપજ કઈ છે ?
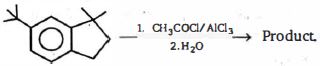
- 95સંયોજન $(A)$ શું હશે ?View Solution
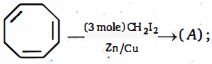
- 96એક દ્રાવણા માટે અભિસરણા (પ૨ાસરણ) દબાણ ($П$) વિરુધ સાંદ્રતા (mol $\mathrm{L}^{-1}$ માં)નો આાલેખ $25.73 \mathrm{~L}$ bar mol ${ }^{-1}$ ઢાળ સાથે સીધી રેખા આપે છે. ક્યા તાપમાન ૫ર અભિસરણા દબાણ આપેલ હતું?View Solution
$\left(\mathrm{R}=0.083 \mathrm{~L}\right.$ bar mol-1 $\mathrm{K}^{-1}$ નો ઉપયોગ કરો)
- 97પાણીમાં ત્રણા વાયુઓ ($A, B, C$)ના હેન્રી નિયમ આચળાંક $\left(\mathrm{K}_{\mathrm{H}}\right)$ મૂલ્યો અનુક્રમ $145,2 \times 10^{-5}$ અને $35 \mathrm{kbar}$ છે પાણીમાં આ વાયુઓની દ્રાવ્યતાઓ કમમાં અનુસરે છે તેView Solution
- 98$10\, \mathrm{~g}$ ગ્લુકોઝ $\left(\mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\right)$ ને $250 \,\mathrm{ml}$ પાણીમાં $\left(\mathrm{P}_{1}\right)$ $10\, \mathrm{~g}$ યુરિયા $\left(\mathrm{CH}_{4} \mathrm{~N}_{2} \mathrm{O}\right)$ ને $250\, ml$ પાણીમાં $\left(\mathrm{P}_{2}\right)$ અને $10\, \mathrm{~g}$ સુક્રોઝ $\left(\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}\right)$ ને $250\, ml$ પાણીમાં $\left(\mathrm{P}_{3}\right)$ ઓગાળીને દ્રાવણો બનાવવામાં આવ્યા. આ દ્રાવણોના અભિસરણ દબાણનો ઘટતો ક્રમ માટેનો સાચો વિકલ્પ પસંદ કરો.View Solution
- 99$45^{\circ} \mathrm{C}$ પર બેન્ઝિન થી ઓકટેનના મોલર ગુણોત્તર $3: 2$ માં દ્રાવણના બાષ્પદબાણના મૂલ્ય માટેનો સાચો વિકલ્પ $\mathrm{Hg}$ નું ...... $\mathrm{mm}$ છે ? [$45^{\circ} \mathrm{C}$ પર બેન્ઝિનનું બાષ્પદબાણ $280\, \mathrm{~mm} \,\mathrm{Hg}$ અને ઓક્ટેનનું $420\, \mathrm{~mm} \,\mathrm{Hg}$ છે. આદર્શ વાયુ ધારી લો.]View Solution
- 100એક વિધુત વિભાજયના $8\,g$ ને $n-$ ઓક્ટેનના $114\,g$ માં દ્રાવ્ય કરવામાં આવે છે , બાષ્પદબાણમાં $80 \%$ નો ઘટાડો કરવા, મોલર દળ ($g\; mol ^{-1}$) માં જણાવો.View Solution
($n-$ ઓક્ટેનનું મોલર દળ $114 \,g\, mol ^{-1}$ આપેલ છે)