$0.2 \mathrm{~kg}$ દળનો પદાર્થ $\left(\frac{25}{\pi}\right) \mathrm{Hz}$ આવૃત્તિ સાથે $\mathrm{x}$-અક્ષની દિશામા: સરળ આવર્ત ગતિ કરે છે. $x=0.04$ સ્થાને પદાર્થની ગતિ ઉર્જા $0.5 \mathrm{~J}$ અને સ્થિતિ ઉર્જા $0.4 \mathrm{~J}$ છે.દોલનનો કંપવિસ્તાર. . . . . . $\mathrm{cm}$.
JEE MAIN 2024, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$8\,cm$ જેટલો સમાન કંપવિસ્તાર અને $10\,Hz$ ની સમાન આાવૃતિ ધરાવતા બે સરળ આવર્ત તરંગો એક દિશામાં ગતિ કરે છે. તેમનો પરિણામી કંપવિસ્તાર પણ $8\,cm$ છે. તો આ તરંગો વચ્યેનો કળા તફાવત $...........^{\circ}$ છે.View Solution
- 2View Solutionસાદા લોલકમાં ધાતુના ગોળાની જગ્યાએ લાકડાનો ગોળો મુક્તા તેનો આવર્તકાળ ....
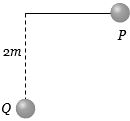
- 3સાદા લોલકને $P$ બિંદુથી મુકત કરતાં તેની $10\%$ ઊર્જા હવાના અવરોધમાં વપરાતી હોય,તો $Q$ બિંદુએ વેગ કેટલો.... $m/sec$ થાય?View Solution
- 4પૃથ્વી પર એક સેકન્ડનો આવર્તકાળ ધરાવતું લોલક એવા ગ્રહ પર લઈ જવામાં આવે છે કે જ્યાં ગુરૂત્વાર્ષણળ બળ $4$ ગણું છે. આ ગ્રહ પર એક સેકન્ડ આવર્તકાળ દર્શાવતા લોલકની લંબાઈ ............ ગણી કરવી જોઈએ ?View Solution
- 5$0.5\, {kg}$ દળ ધરાવતો પદાર્થ સરળ આવર્ત ગતિ કરે છે. જેનો કંપવિસ્તાર $5\, {cm}$ અને આવર્તકાળ $(T)$ $0.2\, {s}$ છે. સમતોલન સ્થાનેથી શરૂ કરીને $t=\frac{T}{4}\;sec$ સમયે પદાર્થની સ્થિતિઉર્જા ($J$ માં) કેટલી હશે?View Solution
દોલનની શરૂઆતની કળા શૂન્ય છે તેમ ધારો.
- 6એક લોલક સરળ આવર્ત ગતિ કરે છે અને મહત્તમ ગતિ ઊર્જા $K_1$ છે. જો લોલકની લંબાઈ બમણી કરવામાં આવે તો તે પ્રથમ કિસ્સામાં જેટલો કંપવિસ્તાર હતો તેટલા જ કપંવિસ્તારથી સરળ આવર્ત ગતિ કરે છે. અને તેની મહત્તમ ગતિ ઊર્જા $K_2$ છે. તો ...View Solution
- 7એક સાદા લોલકને એવી જગ્યાએ મૂકવામાં આવે છે કે જેથી તેનું પૃથ્વીની સપાટી ઉપરથી અંતર પૃથ્વીની ત્રિજ્યા બરાબર થાય. જો દોરીની લંબાઈ $4 m$ હોય તો નાના દોલનોનો આવર્તકાળ_______$s$ થશે. [ $g=\pi^2 m s^{-2}$ લો.]View Solution
- 8$4.84\, N/m$ બળ અચળાંક ધરાવતી સ્પ્રિંગ પર એક $0.98\, kg$ દળનો પદાર્થ દોલનો કરે છે. તો પદાર્થની કોણીય આવૃતિ ($ rad/s$ માં) કેટલી હશે?View Solution
- 9સરળ આવર્ત દોલકનો બળ અચળાંક $2 \times 10^6\, N/m$ અને કંપવિસ્તાર $0.01 \,m $ ની યાંત્રિકઊર્જા $160\,J$ છે. તેની ....View Solution
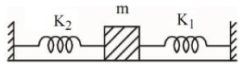
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે $m$ દ્રવ્યમાનને બે દોરી વચ્ચે લગાવેલ છે. બે સ્પ્રિંગોના સ્પ્રિંગ અચળાંક $K_1$ અને $K _2$ છે. ઘર્ષણ મુકત સપાટી પર $m$ દળના દોલનનો આવર્તકાળ છે.View Solution
