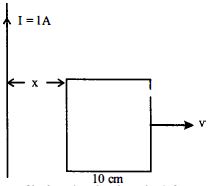
$10\, cm$ બાજુની લંબાઇ ધરાવતી ચોરસ ફ્રેમ અને લાંબો તાર જેમથી $1\, A$ પ્રવાહ વહે છે તેને કાગળના સમતલમાં મૂકેલા છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે ફ્રેમ જમણી બાજુ $10\, ms^{-1}$ ના અચળ વેગથી ગતિ કરે છે. જ્યારે ફ્રેમનો ડાબી બાજુનો છેડો તારથી $x\, = 10\, cm$ અંતરે હોય ત્યારે તેમાં પ્રેરિત થતું $emf$ $\mu V$માં કેટલું હશે?

JEE MAIN 2014, Medium
b
In the given question,
In the given question,
Current flowing through the wire, \(I=1\, A\)
Speed of the frame, \(\mathrm{v}=10\, \mathrm{ms}^{-1}\)
Side of square loop, \(l=10\, \mathrm{cm}\)
Distance of square frame from current carrying
wires \(x=10\, \mathrm{cm}\)
We have to find, \(e.m.f\) inducede =?
According to Biot-Savart's law
\(B = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{Idl\sin \,\theta }}{{{x^2}}}\)
\( = \frac{{4\pi \times {{10}^{ - 7}}}}{{4\pi }} \times \frac{{1 \times {{10}^{ - 1}}}}{{{{({{10}^{ - 1}})}^2}}}\)
\(=10^{-6}\)
Induced \(e.m.f.\) \(\mathrm{e}=\mathrm{Blv}\)
\(=10^{-6} \times 10^{-1} \times 10\)
\(=1 \,\mu v\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$5\,H$ કોઇલમાંથી પ્રવાહના ઘટાડાનો દર $2\, ampere/sec$ હોય તો કોઇલમાં ઉદભવતો $e.m.f. =........V$View Solution
- 2ટોરોઈડમાં આંટા $N =500,$ ત્રિજ્યા $=40$ સેમી અને આડછેદ $10 cm ^{2}$ છે.તેનો ઇન્ડક્ટન્સ શોધો. ($\mu H$ માં)View Solution
- 3$2\, cm$ બાજુની લંબાઈ ધરાવતા એક નક્કર ધાતુનો ઘન,ધન $y -$ દિશામા $6\, m/s$ જેટલી અચળ ઝડપથી ગતિ કરે છે. ધન $z-$ દિશામા $0.1\,T$ પ્રબળતા ધરાવતું એક સમાંગી ચુંબકીય ક્ષેત્ર પ્રવર્તે છે. $x-$ અક્ષને લંબ તેવી ઘનની બે બાજુઓ વચ્ચે સ્થિતિમાનનો તફાવત કેટલા ......$mV$ હશે?View Solution
- 4બે સમકેન્દ્રિય વર્તુળાકાર ગૂચળાં $C _{1}$ અને $C _{2}$ ને $XY$ સમતલમાં મૂકેલા છે. $C _{1}$ માં $500$ આંટા અને ત્રિજ્યા $1 \;cm$ છે. $C _{2}$ માં $200$ આંટા અને ત્રિજ્યા $20\, cm $ છે. $C _{2}$ માંથી સમય પર આધારિત પ્રવાહ $I(t)=\left(5 t^{2}-2 t+3\right)\; A$ વહે છે જ્યાં $t$ $s$ માં છે. $t =1\; s$ સમયે $C _{1}$ માં પ્રેરિત થતો $emf$ ($mV$ માં) $\frac{4}{ x }$ છે. $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 5View Solutionટ્રાન્સફોર્મરનાં ગૌણ ગૂંચળાનો વોલ્ટેજ કોના પર આધારિત નથી.
- 6$P$ અને $Q$ ગુચળાને અમુક અંતરે મૂકેલા છે.જ્યારે $P$ ગુચળામાંથી $3\, A$ પ્રવાહ પસાર થાય ત્યારે $Q$ ગુચળામાંથી $10^{-3}\, Wb$ ચુંબકીય ફ્લક્સ પસાર થાય.$Q$ ગુચળામાંથી કોઈ પ્રવાહ પસાર થતો નથી.જ્યારે $P$ ગુચળામાંથી કોઈ પ્રવાહ પસાર થતો ના હોય અને $Q$ ગુચળામાંથી $2\, A$ પ્રવાહ પસાર થતો હોય ત્યારે $P$ ગુચળામાંથી પસાર થતું ચુંબકીય ફ્લક્સ કેટલું હશે?View Solution
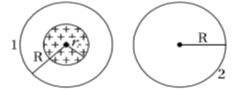
- 7$r $ ત્રિજયાના કોઇ વિસ્તારમાં એકસમાન ચુંબકીયક્ષેત્ર છે. આ ચુંબકીયક્ષેત્રમાં સમય સાથે $\frac{{d\vec B}}{{dt}}$ ના દરથી ફેરફાર થાય છે. આકૃતિમાં દર્શાવ્યા અનુસાર $R$ નું $(R>r) $ લૂપ $-1,r $ ત્રિજયાના લૂપને ઘેરાયેલું છે,તથા $ R$ ત્રિજયાનું લૂપ $- 2$ ચુંબકીયક્ષેત્રના વિસ્તારની બહાર છે. તો ઉત્પન્ન થયેલ $emf$ નું મૂલ્ય કેટલું હશે?View Solution
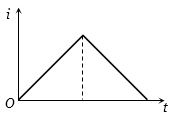
- 8$A.C.$ પરિપથમાં ઇન્ડક્ટર કોઈલનો પ્રવાહ $i$ નો સમય સાથેનો ફેરફાર ગ્રાફમાં બતાવવામાં આવ્યો છે. નીચેનામાંથી કયો આલેખ સમય સાથે વોલ્ટેજને યોગ્ય રીતે રજૂ કરે છે?View Solution
- 9$2\,mH$ અને $8\,mH$ આત્મ-પ્રેરકત્વ ઘરાવતાં બે ગૂંચળાઓ એકબીજાની નજીક એવી રીતે ગોઠવેલાં છે કે જેથી એક ગૂંચળાનું ફ્લકસ બીજા ગૂંચળા સાથે સંપૂર્ણપણે સંકળાય છે. આ બે ગૂંચળા વચ્ચેનું અન્યોન્ય પ્રેરકત્વ ......... $ mH$ હશે.View Solution
- 10$10$ આટાં, $3.6 \times 1 \mathrm{~m}^2$ નું ક્ષેત્રફળ અને $100 \Omega$ નો અવરોધ ધરાવતું એક ચોરસ ગાળો $P Q R S$ ને ધીમેથી (હળવેકથી) અને નિયમીત રીતે $B=0.5 T$ મૂલ્ચ ધરાવતા નિયમીત (સમાન) ચુંબકીય ક્ષેત્રમાંથી દર્શાવ્યા અનુસાર બહાર ખેંચવામાં આવે છે. ગાળાને $1.0 \mathrm{~s}$ માં બહાર ખેંચવામાં કરવું પડતું કાર્ય. . . . . . .$\times 10^{-6} \mathrm{~J}$હશે.View Solution