$10\; cm$ ત્રિજ્યાના એક વાહક ગોળા પર અજ્ઞાત વિદ્યુતભાર છે. ગોળાના કેન્દ્રથી $20\; cm$ દૂરના બિંદુએ વિદ્યુતક્ષેત્ર $-1.5 \times 10^{3} \;N / C$ ત્રિજ્યાવર્તી દિશામાં અંદરની તરફ હોય તો ગોળા પરનો કુલ વિદ્યુતભાર કેટલો હશે?
Medium
b
Electric field intensity \((E)\) at a distance \((d)\) from the centre of a sphere containing net charge \(q\) is given by the relation,
Electric field intensity \((E)\) at a distance \((d)\) from the centre of a sphere containing net charge \(q\) is given by the relation,
\(E=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{d^{2}}\)
Where, \(q=\) Net charge \(=1.5 \times 10^{3} \,N / C\)
\(d =\) Distance from the centre \(=20\, cm =0.2 \,m\)
\(\varepsilon_{0}=\) Permittivity of free space and \(\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \,Nm ^{2} \,C ^{-2}\)
Therefore,
\(=6.67 \times 10^{9}\, C =6.67 \,n\,C\)
\(q=E\left(4 \pi \varepsilon_{0}\right) d^{2}=\frac{1.5 \times 10^{3}}{9 \times 10^{9}}\)
Therefore, the net charge on the sphere is \(6.67 \,n\,C .\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$R$ ત્રિજ્યાના એક અવાહક ગોળાના કદ પર વિદ્યુતભાર $Q$ સમાન રીતે વિતરણ પામેલો છે. $b$ ત્રિજ્યા $(b > R)$ ની પાતળી ધાતુની કવચ વડે ગોળાની આજુબાજુ $-Q$ વિદ્યુતભાર છે. કવચ અને ગોળા વચ્ચેની જગ્યા હવાથી ભરેલી છે. નીચેના પૈકી કયો આલેખ વિદ્યુતક્ષેત્રને સંલગ્ન સાચી રજૂઆત દર્શાવે છે ?View Solution
- 2$10 \,cm$ અને $15 \,cm$ ની બાજુઓ ધરાવતા લંબયોરસ પૃષ્ઠને એકરૂપ વિદ્યુતક્ષેત્ર $25 \,V / m$ માં એવી રીતે મૂકવામાં આવી છે કે જેથી પૃષ્ઠ વિદ્યુતક્ષેત્રની દિશા સાથે $30^{\circ}$ ખૂણો બનાવે તો આ લંબચોરસ પૃષ્ઠમાંથી વિદ્યુતક્ષેત્રનું ફલક્સ ................ $Nm ^2 / C$View Solution
- 3એક તટસ્થ ગોળા પર $10^{12} \,\alpha$ - કણો પ્રતિ સેકન્ડ પડે છે. વિદ્યુતભાર પ્રસ્થાપિત તથા $2\ \mu C$ જેટલો વિદ્યુતભાર પ્રસ્થાપિત થવા માટે કેટલા ......$s$ નો સમય લાગશે?View Solution
- 4$Y$ અક્ષ પર $10^3 \,V/m$ ની સમાન વિદ્યુતક્ષેત્રની ક્ષમતા વિતરણ પામેલી છે. $1\, g$ દળ અને $10^{-6} \,C$ વિદ્યુતભાર વાળો એક પદાર્થ ધન $x$ -અક્ષની દિશામાં ઉગમબિંદુથી ક્ષેત્રમાં $10\,m/s$ ના વેગથી પ્રક્ષેપણ કરે છે. $10\ s$ પછી તેની ઝડપ $m/s$ માં ........ છે.View Solution
- 5$q$ અને $3q$ વિદ્યુતભાર ધરાવતા બે કણો હવામાં $'r' $અંતરે ગોઠવેલા છે. $q$ વિદ્યુતભારથી ' $x$ ' અંતરે વિદ્યુત ક્ષેત્ર શૂન્ય છે. તો $x $નું મૂલ્ય........View Solution
- 6બે પાતળી વિધુતભારિત સમતલ સપાટીની $\sigma_{+}$ પુષ્ઠ ધનતા અને $\sigma_{-}$ છે. જયા $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ બંને સમતલ લંબ છેદે છે. તો તંત્રની વિધુતક્ષેત્ર રેખાનું નિરૂપણView Solution
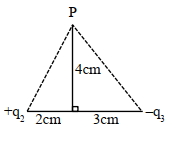
- 7આકૃત્તિમાં દર્શાવ્યા મુજબ, $Y$-અક્ષ પરના $P$ બિંદૂ ઓ પરિણામી વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $\left|\frac{q_2}{q_3}\right|$ નો ગુણોત્તર $\frac{8}{5 \sqrt{x}}$ છે, જ્યાં $x=$. . . . . . .View Solution
- 8ગાઉસનો નિયમ ${ \in _0}\,\oint\limits_{} {\vec E,\,d\vec s\,\, = \,\,q} $ દ્વારા આપવામાં આવે છે જો ગાઉસિયન પૃષ્ઠ વડે ઘેરાતો ચોખ્ખો વિદ્યુતભાર શૂન્ય હોય તો .......View Solution
- 9બે $+9\ e$ અને $+e$ વિદ્યુતભાર ધરાવતા કણો એકબીજાથી $16\, cm$ દૂર આવેલ છે ત્રીજો વિદ્યુતભાર $q$ તેમની વચ્ચે કયાં મુકવો જોઇએ કે જેથી તંત્ર સમતુલનમાં રહે ?View Solution
- 10ઉગમબિંદુ આગળ જેનું કેન્દ્ર હોય તેવા $'a'$ બાજુ વાળો ધન લો. તે $(-q)$ એ $(0, -a/4, 0) પર, (+3q)$ એ $(0, 0, 0)$ પર અને $(-q)$ આગળ ત્રણ નિયત બિંદુવત વિદ્યુતભારથી ઘેરાયેલો છે. સાચો વિકલ્પ પસંદ કરો.View Solution
