\(\mathrm{B}_0\) is the magnetic field at origin
\(\frac{d B}{d x}=-\frac{10^{-3}}{10^{-2}}\)
\(\int_{B_0}^B d B=-\int_0^x 10^{-1} d x\)
\(B-B_0=-10^{-1} x\)
\(B=\left(B_0-\frac{x}{10}\right)\)
Motional emf in \(\mathrm{AB}=0\)
Motional emf in \(\mathrm{CD}=0\)
Motional emf in \(\mathrm{AD}=\varepsilon_1=\mathrm{B}_0 / \mathrm{v}\)
Magnetic field on \(\operatorname{rod} B C B\)
\(=\left(\mathrm{B}_0-\frac{\left(-12 \times 10^{-2}\right)}{10}\right)\)
Motional emf in \(\mathrm{BC}=\varepsilon_2=\left(\mathrm{B}_0+\frac{12 \times 10^{-2}}{10}\right) \ell \times \mathrm{v}\)
\(\varepsilon_{\text {eq }}=\varepsilon_2-\varepsilon_1=300 \times 10^{-7} \mathrm{~V}\)
For time variation
\(\left(\varepsilon_{\text {eq }}\right)^{\prime}=\mathrm{A} \frac{\mathrm{dB}}{\mathrm{dt}}=60 \times 10^{-7} \mathrm{~V}\)
\(\left(\varepsilon_{\text {eq }}\right)_{\text {net }}=\varepsilon_{\text {eq }}+\left(\varepsilon_{\text {eq }}\right)^{\prime}=360 \times 10^{-7} \mathrm{~V}\)
\(\text { Power }=\frac{\left(\varepsilon_{\text {eq }}\right)_{\text {net }}^2}{\mathrm{R}}=216 \times 10^{-9} \mathrm{~W}\)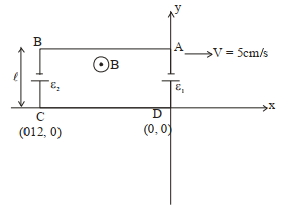
Download our appand get started for free
Similar Questions
- 1એક ગુંચળાનું આત્મપ્રેરિત $emf \,25\,V$ છે, જ્યારે તેમાનો પ્રવાહ સમાન દરથી $1 \,s$ માં $10\, A$ થી $25\, A$ કરવામાં આવે છે. ઊર્જામાં થતો ફેરફાર _____$J$ હશે.View Solution
- 2તારની એક લૂપને ચુંબકીયક્ષેત્રમાં ભ્રમણ કરાવવામાં આવે છે. પ્રેરિત $emf$ ની દિશા બદલવાની આવૃતિ .....View Solution
- 3ગૌણ ગૂંચળામાં આંટાની સંખ્યા $200$ અને પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા $100$ છે.પ્રાથમિક ગૂંચળાને $120\, V$ સાથે લગાવતાં $10 \,A$ પ્રવાહનું વહન થાય છે,તો ગૌણ ગૂંચળાનો વોલ્ટેજ અને પ્રવાહ કેટલો થાય?View Solution
- 4સ્ટેપ ડાઉન ટ્રાન્સફોર્મરને $200\,V$ સાથે લગાવવામાં આવેછે,તેના દ્વારા $6\,V,\,30\,W$ નો બલ્બ શરૂ કરાય છે,તો પ્રાથમિક ગૂંચળામાં પ્રવાહ કેટલા ....$A$ હશે?View Solution
- 5એક ચોક્કસ સ્થિતિસ્થાપક વાહક દ્રવ્યને ખેંયીને વર્તુળાકાર લૂપ બનાવી છે. તેને $B=0.8\,T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રમાં લંબરૂપે મૂકવામાં આવે છે. જ્યારે તેને મુક્ત કરવામાં આવે ત્યારે લૂપનું $2\,cms ^{-1}$ ના અયળ દરે સંકોયન શરૂ થાય છે. તો જ્યારે લૂપની ત્રિજ્યા $10\,cm$ થાય તે વખતે તેમાં પ્રેરિત થતું વીજયાલક બલ $.............$ થશે.View Solution
- 6$10\, ohm$ અવરોધ ધરાવતા બંધ પરિપથનું ચુંબકીય ફલક્સ સમય સાથે $\phi = 6t^2 - 5t +1$ વેબર મુજબ બદલાય છે. $t = 0.25\, s$ એ પ્રેરિત પ્રવાહનું મૂલ્ય ($A$ માં) કેટલું હશે?View Solution
- 7$5\,H$ ઇન્ડકટર અને $10\,Ω$ અવરોઘને $15\, V$ ના $A.C$. ઉદ્ગમ સાથે લગાવવામાં આવે છે.$ t= \infty $ અને $t= 1\,sec$ ના સમયે પ્રવાહનો ગુણોતર કેટલો થાય?View Solution
- 8$100\,mH$ આત્મ-પ્રેરકત્વ ઘરાવતાં ગૂંચળામાં $1 \,A$ પ્રવાહ વહે છે.આ ગૂંચળાના ચુંબકીય ક્ષેત્રમાં કેટલા ......$J$ ઊર્જાનો સંગ્રહ થાય?View Solution
- 9$L$ ઇન્ડકટ્ન્સ ધરાવતા ઇન્ડકટરને બે સમાન ભાગ કરીને સમાંતરમાં જોડતા સમતુલ્ય ઇન્ડકટ્ન્સ શોધો.View Solution
- 10View Solutionસળિયો તેની લંબાઇને લંબ દિશામાં અચળ વેગથી ગતિ કરે છે,ચુંબકીયક્ષેત્ર સળિયા અને વેગને લંબ છે,તો નીચેનામાથી કયું વિધાન સાચું થાય?
