$16 \,cm ^{2}$ જેટલું સમાન આડછેદનું ક્ષેત્રફળ ધરાવતા બે નળાકારીય વાસણો (પાત્રો)માં અનુક્રમે $100 \,cm$ અને $150 \,cm$ ઊંચાઈ સુધી પાણી ભરવામાં આવેલ છે. આ પાત્રોને જોડવામાં આવે છે કે જેથી તેઓમાં પાણીનું સ્તર સમાન ઊંચાઈએ થાય. આ પ્રક્રિયા દરમિયાન ગુરુત્વાકર્ષણને કારણે થતું કાર્ય ..........$J$ થશે. [પાણીની ધનતા $=10^{3} \,kg / m ^{3}$ અને $g =10 \,ms ^{-2}$ લો.]
JEE MAIN 2022, Diffcult
Download our app for free and get started
b
\(h =\frac{ h _{1}+ h _{2}}{2}\)
\(h =\frac{ h _{1}+ h _{2}}{2}\)
Now,
\(W = U _{1}- U _{f}\)
\(W =\left(\rho A h_{1}\right) g \frac{h_{1}}{2}+\left(\rho A h_{2}\right) g \frac{h_{2}}{2}-\rho A \left( h _{1}+h_{2}\right) g\)
\(\left(\frac{h_{1}+h_{2}}{4}\right)\)
\(W =\frac{\rho Ag }{2}\left[ h _{1}^{2}+ h _{2}^{2}-\frac{\left( h _{1}+ h _{2}\right)^{2}}{2}\right]\)
\(W =1\,J\)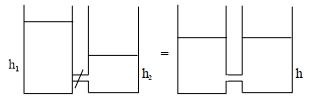
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$0.5\,m$ લંબાઈ ધરાવતો ઘન પાણી પર તરે છે જેનું $30\%$ કદ પાણીની અંદર છે. બ્લોક પર મહત્તમ ......$kg$ વજન મૂકી શકાય કે જેથી તે સંપૂર્ણ પાણીમાં ડૂબી ના જાય. [પાણીની ઘનતા $= 10^3\,kg/m^3$ ]View Solution
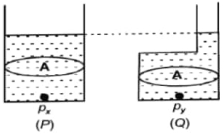
- 2આકૃતિમાં સમાન પાયાનું ક્ષેત્રફળ $A$ સાથેના બે પાત્રો $P$ અને $Q$ દર્શાવેલ છે અને દરેકને સમાન ઊંચાઈ સુધી સમાન પ્રવાહીથી ભરવામાં આવે છે. તેમને અનુરૂપ પસંદ કરો.View Solution
- 3$1.2\,kg\,m^{-3}$ ઘનતા ધરાવતી હવા સમક્ષિતિજ પ્લેનના પાંખડા પર એવી રીતે વહે છે કે જેથી પાંખડાની ઉપર અને નીચે તેનો વેગ $150\,ms^{-1}$ અને $100\,ms^{-1}$ છે,તો પાંખડાની ઉપર અને નીચે દબાણનો તફાવત ........ $Nm^{-2}$ હશે?View Solution
- 4$w$ જાડાઈ ધરાવતા અને $H$ ઊંંચાઈ ધરાવતા ડેમમાં પાણી ભરવામાં આવે છે, તો ડેમ પર લાગુ પડતું પરીણામી બળ.View Solution
- 5લંબાઇ $ M$ દળ ધરાવતા અને $A$ જેટલું આડછેદનું ક્ષેત્રફળ ધરાવતા સમાન નળાકારને તેની લંબાઇ શિરોલંબ દિશામાં રહે તેમ દળરહિત સ્પ્રિંગ વડે નિયત બિંદુ આગળ $\sigma $ જેટલી ઘનતા ધરાવતા પ્રવાહીમાં અડધો ડૂબે તેમ લટકાવવામાં આવે છે,અત્રે નળાકાર સમતોલન સ્થિતિમાં છે.નળાકારની સમતોલન સ્થિતિમાં થતો સ્પ્રિંગની લંબાઇમાં વધારો $x_0$ = ________ થશે.View Solution
- 6નીચે બે વિધાનો આપ્યાં છે.View Solution
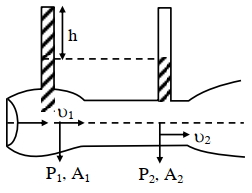
વિધાન $I$: જ્યારે પ્રવાહીની ઝડપ દરેક સ્થાને શૂન્ય હોય તો કોઈ બે બિંદૂઓ વચ્ચેનો દબાણ઼ તફ઼ાવત સમી, $P_1-P_2=\rho g\left(h_2-h_1\right)$ ઊપર આધાર રાખે છે.
વિધાન $II$ : દર્શાવેલ વેન્ચ્યુમીટરમાં $2 \mathrm{gh}=v_1^2-v_2^2$ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો :
- 7રબરના દડાને સમુદ્રના કેટલી ઊંડાઈએ ($m$ માં) લઈ જતાં તેના કદમાં $0.5\, \%$ નો ઘટાડો થાય?View Solution
(રબરનો બલ્ક મોડ્યુલસ $=9.8 \times 10^{8}\, {Nm}^{-2}$, સમુદ્રના પાણીની ઘનતા $=10^{3} {kgm}^{-3}$
$\left.{g}=9.8\, {m} / {s}^{2}\right)$
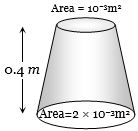
- 8પાત્રમાં ભરેલા પ્રવાહીની ઘનતા $900 kg/m^3$ છે,તો તળિયા પર લાગતું બળ $(g = 10\,m{s^{ - 2}})$ ...... $N$ હશે ?View Solution
- 9$900 Kg/m^3$ ઘનતા ધરાવતો બરફનો ટુકડો $1000 Kg/m^3 $ ઘનતા ધરાવતા પાણીમાં તરે છે,બરફનું ....... $\%$ કદ પાણીની બહાર રહે .View Solution
- 10સ્ટોક્સના નિયમની સકાચણી કરવા માટે કરેલા પ્રયોગમાં $r$ ત્રિજ્યા અને $\rho$ ઘનતા ધરાવતા એક ગોળ દડાને પાણી ભરેલા પાત્રમાં પાણીની સપાટીથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે. જો પાણીની અંદર દડાનો ટર્મિનલ વેગ એ પાણીની અંદર આવતા પહેલા દડાના વેગ જેટલો હોય તો ઊંચાઈ $h$ કોના સમપ્રમાણમાં હશે? (હવાનો શ્યાનતાગુણાંક અવગણો)View Solution