$2 \mathrm{~A}+\mathrm{B} \rightarrow \mathrm{C}+\mathrm{D}$ પ્રક્રિયા ના ગતિકીય અભ્યાસ દરમિયાન, નીચે મુજબ ના પરિણામો પ્રાપ્ત થયા.
| $A[M]$ | $B[M]$ |
સર્જન નો પ્રારંભિક વેગ $D$ |
|
| $i$ | $0.1$ | $0.1$ | $6.0 \times 10^{-3}$ |
| $ii$ | $0.3$ | $0.2$ | $7.2 \times 10^{-2}$ |
| $ii$ | $0.3$ | $0.4$ | $2.88 \times 10^{-1}$ |
| $iv$ | $0.4$ | $0.1$ | $2.40 \times 10^{-2}$ |
ઉપ૨ની માહિતી ના આધારે સમગ્ર પ્રક્રિયાનો ક્રમ ........ છે.
JEE MAIN 2024, Medium
b
$\mathrm{r}=\mathrm{K}[\mathrm{A}]^{\mathrm{x}}[\mathrm{B}]^{\mathrm{y}}$
$\mathrm{r}=\mathrm{K}[\mathrm{A}]^{\mathrm{x}}[\mathrm{B}]^{\mathrm{y}}$
$(I)$ $6 \times 10^{-3}=\mathrm{K}[0.1]^{\mathrm{x}}[0.1]^{\mathrm{y}}$
$(IV)$ $2.4 \times 10^{-2}=\mathrm{K}[0.4]^{\mathrm{x}}[0.1]^{\mathrm{y}}$
$(IV)/(I)$
$4=(4)^{\mathrm{x}}$
$\mathrm{x}=1$
$\mathrm{r}=\mathrm{K}[\mathrm{A}]^{\mathrm{x}}[\mathrm{B}]^{\mathrm{y}}$
$(III)$ $2.88 \times 10^{-1}=\mathrm{K}[0.3]^{\mathrm{x}}[0.4]^{\mathrm{y}}$
$(II)$ $7.2 \times 10^{-2}=\mathrm{K}[0.3]^{\mathrm{x}}[0.2]^{\mathrm{y}}$
$(III)/(II)$
$4=2^y$
$y=2$
Overall order $=x+y=1+2=3$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રકિયા ${A_{\left( g \right)}} + 3{B_{\left( g \right)}} \to 2{C_{\left( g \right)}}$ માટે $- d[A]/dt$ નુ મૂલ્ય $3 \times 10^{-3}\, mol\, L^{-1}\,min^{-1}$ હોય, તો $- d[B[dt$ નુ મૂલ્ય .... થશે.View Solution
- 2પ્રથમ ક્રમની પ્રક્રિયા માટે, ધન ઢાળ મેળવવા માટે કયા ઢાળ ની જરૂર છે( જ્યાં $[A]$ એ પ્રકીયક ની સાંદ્રતા $A$)View Solution
- 3એક રેડિયોએક્ટિવ તત્વનો અર્ધ આયુષ્ય $200 \,days$ (દિવસો) છે. $83 \,days$ (દિવસો) પછી બાકી રહેલ મૂળ સક્રિયતાની ટકાવારી $.....$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : એન્ટીલોગ $antilog$ $0.125=1.333$,
$\text { antilog } 0.693=4.93 \text { ) }$
- 4View Solutionનીચેના ગ્રાફ માટે,
નીચે આપેલા વિકલ્પોમાંથી પસંદ કરો, પ્રક્રિયાના ક્રમમાં કયો સંબંધિત સાચો છે:
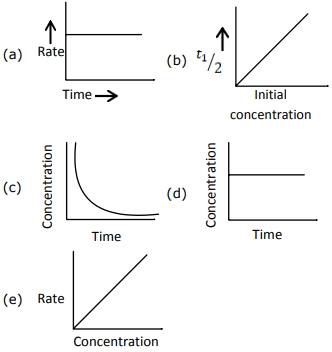
- 5પ્રથમ ક્રમમાં રાસાયણિક પ્રક્રિયાનો અર્ધ આયુષ્ય સમય $6. 93\,\min$. છે $99\%$ પ્રકિયા પૂર્ણ થવા માટે લાગતો સમય કેટલો છે ?View Solution
- 6$A + B \rightarrow $ નિપજ, પ્રક્રિયા માટે $A$ ના સંદર્ભમાં ક્રમ $1$ છે અને $B$ ના સંદર્ભમાં ક્રમ $1/2 $ છે. જ્યારે $A$ અને $B$ બંનેની સાંદ્રતા ચાર ગણી વધે છે. તો દર એ ....... ગુણાંક વધે છે.View Solution
- 7પ્રથમ ક્રમ પ્રકમમાં વાયુમય સાયક્લો બ્યુટીનના બ્યુટાડાઈનમાં સમઘટકીકરણ (isomerizes) થાય છે કે જેનું $153°C$ પર, $‘k’$ મૂલ્ય $3.3 \times 10^{-4} s ^{-1}$ છે. તો આ જ તાપમાને $40\%$ સમઘટકીકરણ પૂર્ણ કરવા માટે લાગતો સમય મિનીટોમાં ........... છે. (નજીકના પૂર્ણાંકમાં રાઉન્ડ ઓફ કરવું)View Solution
- 8$A \rightarrow B$ રાસાયણિક પ્રક્રિયા માટે, એવું જાણવા મળ્યું કે $B$ ની સાંદ્રતા $0.2\, mol\,L^{-1}$ $30\, {~min}$માં વધી છે. પ્રક્રિયાનો સરેરાશ વેગ $......\times 10^{-1} {~mol} {~L}^{-1} {~h}^{-1}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
- 9પ્રથમ ક્રમની પ્રક્રિયા $90\%$ પુરી થવા સમય $40$ મિનિટ લાગે છે. તો પ્રક્રિયાનો અર્ધઆયુષ્ય .....View Solution
- 10પ્રથમક્રમની પ્રક્રિયા માટે શરૂઆતની સાંદ્રતામાં $1/4$ જેટલો ઘટાડો થવા માટે લાગતો સમય $20$ મિનિટ છે. તો શરૂઆતની સાંદ્રતા માં $1/16 $ જેટલો ઘટાડો થવા માટે લાગતો સમય......... $\min.$ હશે.View Solution
