For first order reaction
\(k=\frac{2.303}{t} \log \frac{100}{100-99}\)
\(\frac{0.693}{6.93}=\frac{2.303}{t} \log \frac{100}{1}\)
\(\frac{0.693}{6.93}=\frac{2.303 \times 2}{t}\)
\(\Rightarrow t=46.06\, \mathrm{min}\)
Download our appand get started for free
Similar Questions
- 1ક્લોરિન પરમાણુઓની હાજરીમાં ઓઝોનની ઓકિસજન પરમાણુઓ સાથેની પ્રક્રિયા નીચે દર્શાવેલ બે તબક્કા મુજબ થઈ શકે છે.View Solution
${O_3}(g)\, + \,C{l^ * }(g)\, \to \,{O_2}(g) + Cl{O^ * }(g)$ ..... $(i)$ $[{K_i} = 5.2 \times {10^9}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
$Cl{O^ * }(g) + {O^ * }(g)\, \to \,{O_2}(g) + \,C{l^ * }(g)$ ..... $(ii)$ $[{K_{ii}} = 2.6 \times {10^{10}}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
તો સમગ્ર પ્રક્રિયા ${O_3}(g){\mkern 1mu} + {\mkern 1mu} {O^*}(g){\mkern 1mu} \to {\mkern 1mu} 2{O_2}(g)$ માટે સમગ્ર પ્રક્રિયાનો વેગ .......... $L\,\,mo{l^{ - 1}}\,{s^{ - 1}}$ અચળાંક કોની સૌથી નજીક હશે ?
- 2$A + B \rightarrow $ નિપજ પ્રક્રિયા માટેનો દર નિયમ દર $= K[A]^1[B]^2$ છે. તો નીચેનામાંથી કયું વિધાન ખોટું છે?View Solution
- 3View Solutionવાયુરૂપ પ્રક્રિયા માટે તાપમાનમાં થોડો વધારો કરતા વેગમાં થતો મોટો વધારો ...... સૂચવે છે.
- 4એક પ્રક્રિયા વેગ-અચળાંક $K_1$ અને $K_2$ અનુક્રમે $10^{16}.e^{-2000/T}$ અને $10^{15}.e^{-1000/T } $ છે, તો ક્યા તાપમાને $K_1 = K_2$ થશે ?View Solution
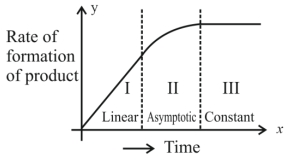
- 5એક નિશ્ચિત રાસાયણિક પ્રક્રિયા $X \rightarrow Y$ માટે, નીપજના બનવાનો દર વિરુદ્ધ સમયનો ગ્રાફ (આલેખ) એ આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચાં વિધાન/નોની સંખ્યા $..............$ છે.View Solution
$(A)$ સમગ્ર પ્રક્રિયાનો ક્રમ છે.
$(B)$ આ પ્રક્રિયાનો ક્રમ શોધી શકાતો નથી.
$(C)$ $I$ અને $III$ વિભાગ માં, પ્રક્રિયા અનુક્રમે પ્રથમ અને શૂન્ય ક્રમની છે.
$(D)$ વિભાગ $II$ માં, પ્રક્રિયા પ્રથમક્રમની છે.
$(E)$ વિભાગ $II$ માં, પ્રક્રિયાનો ક્રમ $0.1$ થી $0.9$ વિસ્તાર માં છે.
- 6View Solutionપ્રથમક્રમની પ્રક્રિયા માટે વેગ અચળાંકનો એકમ નીચેના પૈકી કયો હશે ?
- 7દ્વિતીય ક્રમ પ્રક્રિયા માટે કે જેના બંને પ્રક્રિયકો સમાન પ્રારંભિક સાંદ્રતા ધરાવે છે અને પ્રક્રિયા $20\%$ પુરી થવા માટે $500$ સેકન્ડ લાગે છે. તો પ્રક્રિયાને $80\%$ પુરી થવા ......... સેકન્ડ લાગશે.View Solution
- 8પ્રથમક્રમની એક પ્રક્રિયામાં $2 × 10^4$ સેકન્ડમાં પ્રક્રિયાની સાંદ્રતા $800$ મોલ/ડેસીમી $^3$ થી ઘટીને $50$ મોલ/ડેસીમી $^3$ થાય છે. તો પ્રક્રિયાનો વેગ-અચળાંક કેટલો થશે ?View Solution
- 9View Solutionટંગસ્ટનની સપાટી પર અધિશોષણ થવાથી વાયુ ઉત્પન્ન થવાની પ્રક્રિયા .. ક્રમની છે.
- 10બે પ્રક્રિયાઓ $R_1$ અને $R_2$ ના પૂવઘાતાંકીય અવયવો સમાન છે. $R_1$ ની સક્રિયકરણ ઊર્જા $R_2$ કરતા $10\, kJ\,mol^{-1}$ વધારે છે. $300 \,K$ તાપમાને પ્રક્રિયાઓ $R_1$ અને $R_2$ ના વેગ અચળાંક અનુક્રમે $k_1$ અને $k_2$ હોય, તો $\ln (k_2/k_1)$ કોને સમાન થશે ?View Solution
