$2 \,m$ લંબાઈ અને $1 \,cm ^2$ આડછેદ ધરાવતા તારનુ તાપમાન $0^{\circ} C$ થી $80^{\circ} C$ સુધી લઈ જવામા આવે છે અને આના લીધે લંબાઈમાં વધારો થતો ન હોય તો જરૂરી બળ કેટલુ લગાવુ જોઈએ? $\left\{Y=10^{10} \,N / m ^2, \alpha=10^{-6} /^{\circ} C \right\}$
Easy
a
(a)
(a)
Thermal expansion would be \(=L \propto \Delta T\)
Where \(L=\) original length
\(\alpha=\) coefficient of linear expansion
\(\Delta T=\) Change in temperature
So substituting values
\(\Delta L=2 \times 10^{-6} \times 80\)
\(\Delta L=1.6 \times 10^{-4} \,m\)
Now \(\Delta L=\frac{F L}{A Y}\)
\(\frac{\Delta L \times A Y}{L}=F\)
Substitute values
\(\frac{1.6 \times 10^{-4} \times 10^{10} \times 1}{2 \times 10000}=F\)
\(80 \,N = F\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો સ્પ્રિંગને $l$ લંબાઈ સુધી ખેચવામાં આવે તો હુકના નિયમ અનુસાર નીચેનામાથી શું સાચું છે ?View Solution
- 2સિલ્વર માટે યંગ મોડયુલસ $7.25 \times {10^{10}}\,N/{m^2}$ અને બલ્ક મોડયુલસ $11 \times {10^{10}}\,N/{m^2}$ હોય,તો પોઇસન ગુણોત્તર કેટલો થાય ?View Solution
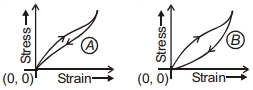
- 3View Solutionબે જુદા જુદા પ્રકારના રબર માટે પ્રતિબળ - વિકૃતિનો વક્ર આપેલ છે. તો
- 4એક નક્કર સમઘન તાંબાની બનેલી છે અને તેની બાજુનું માપ $10 \,cm$ છે. તેમા આપવામા આવતુ હાઈડ્રોલીક દબાણ $7 \times 10^6$ pascal છે. જો તારનો બલ્ક મોડ્યુલસ $140 \,GPa$ હોય તો કદમાં થતુ સંકોચન .............. $m ^3$View Solution
- 5એક લોખંડના સળિયાની ત્રિજ્યા $20\,mm$ અને લંબાઈ $2.0\,m$ છે.$62.8\,kN$ નું બળ તેમની લંબાઈને સાપેક્ષે ખેંચે છે. લોખંડનો યંગ અચળાંક $2.0 \times 10^{11}\,N / m ^2$ છે. તારમાં ઉત્પન્ન થતી પ્રતાન વિકૃતિ ........ $\times 10^{-5}$ છે.View Solution
- 6$2\, m$ લંબાઈ અને $10\;c{m^3}$ આડછેડનું ક્ષેત્રફળ ફ્ધારવતા કોપરના તાર પર $F$ બળ લગાવતા તેની લંબાઈમાં $2\, mm$ નો વધારો થાય છે. બીજા સમાન કદ ધરાવતા કોપરનો તાર જેની લંબાઈ $8 \,m$ છે તેના પર $F$ બળ લગાવતા લંબાઈમાં થતો વધારો ......... $cm$ હશે .View Solution
- 7View Solutionહુકનો નિયમ શું વ્યાખ્યાયિત કરે છે ?
- 8$0.1 \,m$ બાજુવાળા સમઘન બ્લોકની ઉપરની બાજુ પર $100 \,N$ નું સ્પર્શીય બળ લગાડતાં તે નીચેની બાજુની સાપેક્ષે $0.02 \,cm$ ખસે છે,તો સ્પર્શીય વિકૃતિ કેટલી થાય?View Solution
- 9View Solutionસ્પર્શીય પ્રતિબળને લીધે શેમાં ફેરફાર થાય છે ?
- 10View Solutionબલ્ક મોડ્યુલસ સૌપ્રથમ કોના દ્વારા વ્યાખ્યાયિત કરવામાં આવ્યો હતો ?
