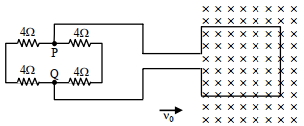
$20\, {cm}$ બાજુવાળી અને $1\, \Omega$ અવરોધ ધરાવતી ચોરસ લૂપ ${v}_{0}$ જેટલી અચળ ઝડપથી જમણી બાજુ ગતિ કરે છે. લૂપની જમણી બાજુ $5\, {T}$ ના મૂલ્યનું એકસમાન ચુંબકીયક્ષેત્ર છે. આ ક્ષેત્ર લૂપના સમતલને લંબ અને અંદર તરફની દિશામાં છે. આ લૂપ દરેક $4\, \Omega$ અવરોધ ધરાવતા નેટવર્ક સાથે જોડાયેલ છે. લૂપમાંથી $2\, {mA}$ ના અચળ પ્રવાહનું વાહન કરાવવા માટે $v_{0}$ નું મૂલ્ય કેટલું હોવું જોઈએ?
JEE MAIN 2021, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$100\,cm^2$ ક્ષેત્રફળ અને $50$ આંટા ધરાવતી કોઇલ પર $2 \times 10^{-2}\, T $ જેટલું ચુંબકીય ક્ષેત્ર લંબરૂપે લાગે છે. જ્યારે કોઇલને $t$ સમયમાં ક્ષેત્રની બહાર લઈ જવામાં આવે, ત્યારે પ્રેરિત $emf$ નું મૂલ્ય $0.1\,V$ છે. $t$ નું મૂલ્ય સેકન્ડમાં કેટલું હશે?View Solution
- 2$10$ આંટાની કોઈલ અને $20\;\Omega$ અવરોધ એ $30 \Omega$ અવરોધ $B, G$ સાથે શ્રેણીમાં જોંડેલ છે. $10^{-2}$ નિયમિત ચુંબકીય ક્ષેત્ર પ્રેરણ સાથે તે સમતલ લંબ રહે તેમ તે કોઈલ મૂકેલી છે. હવે તેને $60^{\circ}$ ના ખૂણે ફેરવવામાં આવે છે. કોઈલમાં ઉદ્ભવેલો વીજભાર $..............\times 10^{-5}\,C$ (કોઈલનું ક્ષેત્રફળ = $\left.10^{-2}\,m ^2\right)$View Solution
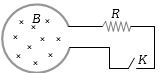
- 3ચુંબકીયક્ષેત્રનો ફેરફાર $B = {B_0}{e^{ - t}}$ મુજબ થાય છે,કોઇલની ત્રિજયા $r$ અને અવરોધ $R$ છે.તો કળ ($K$) બંધ કરતાં કેટલો પાવર ઉત્પન્ન થાય?View Solution
- 4સ્ટેપ અપ ટ્રાન્સફોર્મરમાં પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા અને ગૌણ ગૂંચળામાં આંટાની સંખ્યાનો ગુણોત્તર $1:2$ છે,પ્રાથમિક ગૂંચળા સાથે $1.5 \,V$ લેકલાન્સ કોષ જોડતાં ગૌણ ગૂંચળાનો વોલ્ટેજ કેટલા .......$V$ થાય?View Solution
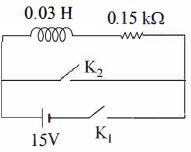
- 5નીચે દર્શાવેલ પરિપથમાં એક ઇન્ડકટર $(L=0.03H)$ અને અવરોધ $(R=0.15$ $K\Omega)$ એક $15$ $V$ $emf$ ધરાવતી બેટરી સાથે શ્રેણીમાં જોડેલા છે.કળ $K_1$ ને ઘણા લાંબા સમય સુધી બંધ રાખવામાં આવે છે.પછી, $t=0$ સમયે કળ ને ખોલવામાં $(open)$ આવે છે અને તે જ સમયે કળ $K_2$ ને બંધ $(close)$ કરવામાં આવે છે.$t= 1$ $ms$ ને અંતે પરિપથમાં વહેતો પ્રવાહ .......... $mA$ હશે. (${e^5} \cong 150)$View Solution
- 6ચુંબકને કોઇલ તરફ $(i)$ ઝડપી અને $(ii)$ ધીમેથી ગતિ કરાવતાં ઉત્પન્ન થતું $emf$ અને વિદ્યુતભાર અનુક્રમે...View Solution
- 7$0.4\;m$ લંબાઇનો વાહક સળિયો એ $0.9\;Wb/m^2$ જેટલા ચુંબકીય ક્ષેત્રમાં ચુંબકીયક્ષેત્રને લંબદિશામાં $7\;m/s$ ની ઝડપથી ગતિ કરે છે. વાહકના છેડે પ્રેરિત $e.m.f$ કેટલા $V$ હશે?View Solution
- 8$\mathrm{R}$ ત્રિજ્યા ધરાવતો લાંબો સોલેનોઇડ સમય સાથે ફરતા પ્રવાહ $\mathrm{I}(\mathrm{t})=\mathrm{I}_{0} \mathrm{t}(1-\mathrm{t})$ નું વહન કરે છે. $2 \mathrm{R}$ ત્રિજ્યાની રિંગને તેને સમઅક્ષીય રીતે રહે તેમ તેના મધ્યમાં મૂકવામાં આવે છે. $0 \leq t \leq 1$,સમય દરમિયાન રિંગમાં પ્રેરિત પ્રવાહ $\left(\mathrm{I}_{\mathrm{R}}\right)$ અને પ્રેરિત $\mathrm{EMF}\left(\mathrm{V}_{\mathrm{R}}\right)$ કઈ રીતે બદલાય?View Solution
- 9$1\, meter$ ત્રિજ્યા ધરાવતી રીંગ $0.01\,T$ના ચુંબકીય ક્ષેત્રમાં લંબ રહીને $100\,Hz$ આવૃતિથી દોલન કરે તો તેમાં ઉદભવતું વિદ્યુતક્ષેત્ર ..... $Volt/m$View Solution
- 10$R$ ત્રિજયાવાળી અર્ધવતુળાકાર રીંગ $B$ ચુંબકીયક્ષેત્રમાં $V$ વેગથી ગતિ કરે છે.તો તેમાં ઉદ્ભવતું $emf$ ...View Solution
