Given area of Parallel plate capacitor, \(A=\) \(200\, \mathrm{cm}^{2}\)
Separation between the plates, \(d=1.5\, \mathrm{cm}\) Force of attraction between the plates, \(F=\) \(25 \times 10^{-6}\, \mathrm{N}\)
\(F=Q E\)
\(F=\frac{Q^{2}}{2 A \epsilon_{0}} \quad\) (\(E\) due to parallel plate
\(=\frac{\sigma}{2 \epsilon_{0}}=\frac{Q}{A 2 \epsilon_{0}})\)
But \(Q=C V=\frac{\epsilon_{0} A(V)}{d}\)
\(\therefore \,F = \,\frac{{({\epsilon_0}A{V^2})}}{{{{\text{d}}^2} \times 2{\text{A}}{\epsilon_0}}}\)
\( = \frac{{{{\left( {{\epsilon_0}A} \right)}^2} \times {V^2}}}{{{d^2} \times 2 \times \left( {A{\epsilon_0}} \right)}} = \frac{{\left( {{\epsilon_0}A} \right) \times {V^2}}}{{{d^2} \times 2}}\)
or, \(25 \times {10^{ - 6}} = \frac{{\left( {8.85 \times {{10}^{ - 12}}} \right) \times \left( {200 \times {{10}^{ - 4}}} \right) \times {V^2}}}{{2.25 \times {{10}^{ - 4}} \times 2}}\)
\( \Rightarrow V\, = \frac{{25 \times {{10}^{ - 6}} \times 2.25 \times {{10}^{ - 4}} \times 2}}{{8.85 \times {{10}^{ - 12}} \times 200 \times {{10}^{ - 4}}}}\) \( \approx 250\,V\)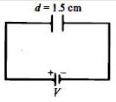
Download our appand get started for free
Similar Questions
- 1View Solutionવિદ્યુતભારીત કેપેસીટરની સંગ્રહીત ઊર્જા કયા સૂત્ર દ્વારા આપી શકાય ?
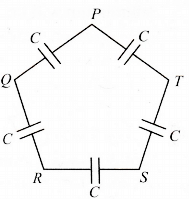
- 2$C$ કેપેસીટન્સ ધરાવતા પાંચ કેપેસીટરને આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલા છે. તો $P$ અને $R$ તથા $P$ અને $Q$ વચ્ચેના કેપેસીટન્સનો ગુણોત્તર કેટલો થાય?View Solution
- 3અવકાશમાં $\vec E\, = (25 \hat i + 30 \hat j)\,NC^{-1}$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. જો ઉગમબિંદુ આગળ વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $x\, = 2\, m, y\, = 2\, m$ બિંદુ આગળ વિદ્યુતસ્થિતિમાન $volt$ માં કેટલું મળે?View Solution
- 4એક વિસ્તારમાં વિદ્યુત સ્થિતિમાન દર્શાવવા માટે $V=\frac{3 x^2}{2}-\frac{y^2}{4}$ સંબંધ વપરાય છે.$x$ અને $y$ મીટરમાં છે અને $V$ એ વૉલ્ટમાં છે. તો બિંદુ $(1\,m,2\,m)$ પર વિદ્યુતક્ષેત્રની તિવ્રતા $N / C$ કેટલી થશે ?View Solution
- 5સમાંતર પ્લેટ કેપેસીટરની પ્લેટ વચ્ચે ડાઈઇલેક્ટ્રિક મૂકવામાં આવે છે. જેનો ડાઈઇલેક્ટ્રિક અચળાંક નીચે મુજબ બદલાય છે.View Solution
$K(x) = K_0 + \lambda x$ ($\lambda =$ અચળાંક)
શૂન્યાવકાશમાં કેપેસીટરનું મૂલ્ય $C_0$ હોય તો $C_0$ના સ્વરૂપમાં કેપેસીટન્સ $C$ કેટલું મળે?
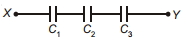
- 6આકૃતિમાં $C_1=20 \mu F , C_2=40 \mu F$ અને $C_3=50 \mu F$ દર્શાવેલ છે. જો કોઈ પણ કેપેસીટર $50 \,V$ થી વધુનું સ્થિતિમાન ધારણ કરી શકતો ન હોય તો બિંદુ $X$ અને $Y$ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત મેળવો.View Solution
- 7સમાંતર પ્લેટ કેપેસીટરની બે પ્લેટ વચ્ચે $200 \Omega \, {m} $ અવરોધકતા ધરાવતો પદાર્થ ભરેલો છે.કેપેસીટરના કેપેસીટન્સનું મુલ્ય $2\, {pF}$ છે. જો કેપેસીટરની બે પ્લેટ વચ્ચે $40 \,{V}$ નો વિદ્યુતસ્થિતિમાનનો તફાવત લાગુ પાડવામાં આવે તો, કેપેસીટરમાંથી લીકેજ થતો પ્રવાહ કેટલો હશે?View Solution
(પદાર્થની સાપેક્ષ પરમીએબિલિટી $50$ છે)
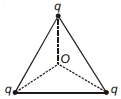
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે, ત્રણ ચાર્જને અને સમબાજુ ત્રિકોણના ખુણાઓ પર મુકેલ છે. આ ત્રિકોણના કેન્દ્ર માટે કયું વિધાન;તેના કુલ સ્થિતિમાન $V$ અને વિદ્યુત ક્ષેત્ર $E$ માટે સત્ય છે ?View Solution
- 9$4\,cm$ જેટલી પ્લેટોની પહોળાઈ, લંબાઈ $8\,mm$, અને બે પ્લેટો વરચેનું અંતર $4\,mm$ હોય તેવા સમાંતર પ્લેટ સંઘારકને $20\,V$ ની બેટરી સાથે જોડવામાં આવે છે. $5$ જેટલો ડાયઈલેક્ટિક્ર અચળાંક ધરાવતો અને $1\,cm$ લંબાઈ, $4\,cm$ પહોળાઈ અને $4\,mm$ જાડાઈ ધરાવતા ડાયઈલેક્ટ્રિક માધ્યમને સંઘારકની પ્લેટોની વરચે દાખલ કરવામાં આવે છે. આ તંત્ર માટે સ્થિત વિદ્યુત ઊર્જા $........\varepsilon_0 J$ થશે.(જ્યાં $\varepsilon_0$ શુન્યાવકાશની પરમીટીવીટી છે)View Solution
- 10એક સમાંતર પ્લેટ કેપેસિટર પાસે $20\, kV$ સ્થિતિમાન અને $2 \times 10^{-4} \,\mu F$ કેપેસિટન્સ છે. જો પ્લેટનું ક્ષેત્રફળ $0.01\, m^2$ હોય અને પ્લેટો વચ્ચેનું અંતર $2\ mm$ હોય તો માધ્યમનું ડાઈઈલેકટ્રીક અચળાંક શોધો.View Solution
