ઉદ્દીપકની ગેરહાજરીમાં અચળાંક \(= k_1,\)
ઉદ્દીપકની હાજરીમાં દર અચળાંક \(= k_2\)
ઉદ્દીપકની ગેરહાજરીમાં સક્રિયકરણ ઊર્જા \( (E_1) = 30\,kJ\) મોલ \(^{-1} \) ,
ઉદ્દીપકની હાજરીમાં સક્રિયકરણ ઊર્જા \((E_1) = 24\,kJ\) મોલ \(^{-1}\)
સક્રિયકરણ ઊર્જાનો સિધ્ધાંત મુજબ,
\({k_1} = A{e^{ - {E_1}/RT}}\) ;
\({k_2} = A{e^{ - {E_2}/RT}}\)
\(\frac{{{k_2}}}{{{k_1}}}= {e^{({E_1} - {E_2})R/T}}\) OR \(\frac{{{k_2}}}{{{k_1}}} = \frac{{{E_1}\, - \,{E_2}}}{{RT}}\)
\(\log \frac{{{k_2}}}{{{k_1}}}{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{E_1}{\mkern 1mu} - {\mkern 1mu} {E_2}}}{{2.303RT}}{\mkern 1mu} \)
\( = {\mkern 1mu} {\mkern 1mu} \frac{{(30{\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} {\mkern 1mu} 24){\mkern 1mu} {\mkern 1mu} \times {\mkern 1mu} {\mkern 1mu} {{10}^3}{\mkern 1mu} J{\mkern 1mu} \,mo{l^{ - 1}}}}{{2.303{\mkern 1mu} \times {\mkern 1mu} (8.314\,J\,{K^{ - 1}}{\mkern 1mu} mo{l^{ - 1}}){\mkern 1mu} \times {\mkern 1mu} 298{\mkern 1mu} \,K}}\)
\(\frac{{{k_2}}}{{{k_1}}}\,\, =\) Antilog \(1.0516= 11.27\) or \({k_2} = 11.27\,{k_1}\)
જેથી, પ્રક્રિયાનો દર \(11 \) ગણો જેટલો.
Download our appand get started for free
Similar Questions
- 1$2A\rightarrow$ નિપજ પ્રથમ ક્રમ ગતિકી દર્શાવે છે જો $[A]$ Initial $= 0.2$ મોલ લીટર $^{-1}$ પ્રક્રિયાનો અદ્ય આયુષ્ય સમય $20 $ મિનિટ છે. તો દર અચળાંક નું મુલ્ય શોધો.View Solution
- 2પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે સંકલીત વેગ નિયમ ક્યા સમીકરણથી દર્શાવી શકાય છે. (જ્યાં $P_i=$ પ્રારંભિક દબાણ, $\mathrm{P}_{\mathrm{t}}=\mathrm{t}$ સમયે કુલ દબાણ)View Solution
- 3પ્રથમ ક્રમની પ્રક્રિયા $A → B$ માટે દર અયળાંક $k =5.5 \times 10^{-14} s ^{-1} .67 \%$ પૂર્ણ થવા માટેનો જરૂરી સમય તેના પ્રક્રિયાના અર્ધ આયુષ્ય કરતા $x \times 10^{-1}$ ગણો છે. તો $x$ નું મૂલ્ય $\dots\dots$છે.View Solution
- 4$300\,^o C$ તાપમાને પ્રથમ કમની એક પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા $35\, kcal\, mol^{-1}$ અને આવૃત્તિ અવયવ $1.45 \times 10^{-11}\,s^{-1}$ છે, તો વેગ અચળાંક જણાવો.View Solution
- 5View Solutionપ્રક્રિયા દરની સંઘાત પદ્ધતિના આધારે.....
- 6$2FeCl_3 + SnCl_2 \rightarrow 2FeCl_2 + SnCl_4 $ આપેલ પ્રક્રિયા ....... નું ઉદાહરણ છે.View Solution
- 7આપેલ આલેખ બે જુદી જુદી પ્રક્રિયા $(i)$ અને $(ii)$ માટે સમય સાથે પ્રક્રિયક $R$ ની સાંદ્રતાનો ફેરફાર રજૂ કરે છે. તી પ્રક્રિયાના ક્રમ અનુક્રમે જણાવો.View Solution
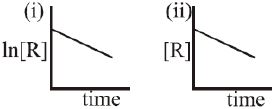
- 8સંસ્પર્શ પ્રક્રિયા દ્વારા $ 2SO_2 (g) + O_2(g) \rightarrow 2SO_3(g)$ સલ્ફર ટ્રાયોક્સાઈડનાં નિર્માણમાં તે પ્રક્રિયાનો દર $-\frac{d({{O}_{2}})}{dt}=2.5\times {{10}^{-4}}\,mol\text{ }{{L}^{-1}}{{\sec }^{-1}}$ છે. તો તેના $(SO_2) $ નો અપારદર્શક દર કેટલો થશે?View Solution
- 9પ્રકિયા માટે ${N_2}{O_5}(g) \to $ $2N{O_2}(g) + \frac{1}{2}{0_2}(g)$ વેગ અચળાંક k, $2.3 \times {10^{ - 2}}\,{s^{ - 1}}$.છે નીચે આપેલું કયું સમીકરણ સમય સાથે $[{N_2}{O_5}]$ ના ફેરફારનું વર્ણન કરે છે?${[{N_2}{O_5}]_0}$ અને ${[{N_2}{O_5}]_t}$ પ્રારંભિક અને સમય પર ${N_2}{O_5}$ ની સાંદ્રતાને અનુરૂપ છે.View Solution
- 10પ્રથમ ક્રમની પ્રક્રિયા $N_2O_5$ (in $CCl_4$) $\rightarrow 2NO_2 + {1/2}O_2(g)$ એ $N_2O_5 $ નાં સંદર્ભમાં અને $6.2 \times 10^{-4}\,S^{-1}$ દર અચળાંક ધરાવે છે. તો જ્યારે $[N_2O_5] = 1.25 $ મોલ $L^{-1}$ હોય તો પ્રક્રિયા દર શું થશે?View Solution
