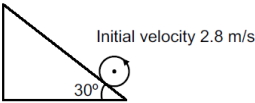
The acceleration of a sphere down the inclined plane is given
by,
\(a=\frac{g \sin \theta}{1+\frac{k^{2}}{r^{2}}}\)
The moment of inertia of the sphere is given by,
\(I=\frac{2}{5} m r^{2}\)
\(=m k^{2}\)
Consider above,
\(\frac{k^{2}}{r^{2}}=\frac{2}{5}\)
Use the equation,
\(v^{2}=2 a s\) \(...(I)\)
Substitute \(2.8\) for \(v, \frac{2}{5}\) for \(\frac{k^{2}}{r^{2}}, 30^{\circ}\) for \(\theta\) and \(\frac{g \sin \theta}{1+\frac{k^{2}}{r^{2}}}\) for \(a\) in
equation \((I)\)
\(2.8^{2}=2\left(\frac{g \sin 30^{\circ}}{1+\frac{2}{5}}\right) s\)
\(=2\left(\frac{2(10)\left(\frac{1}{2}\right)}{\frac{7}{2}}\right)\)
\(s=2.8^{2}\left(\frac{7}{20}\right)\)
\(=2.744 m\)
Download our appand get started for free
Similar Questions
- 1$m$ દળના કણની સમય $t$ સાથે નીચે મુજબ ગતિ કરે છે.View Solution
$\overrightarrow{{r}}=10 \alpha {t}^{2}\, \hat{{i}}+5 \beta({t}-5)\, \hat{{j}}$
જ્યાં $\alpha$ અને $\beta$ પરિમાણવાળા અચળાંક છે. કણનું કોણીય વેગમાન ${t}=0$ સમયે હોય તેટલું ફરીથી $t=$ .....$seconds$ સમયે થશે.
- 2નકકર ગોળો વ્યાસને અનુલક્ષીને ફરે છે. તાપમાન વઘવાથી તેના કદમાં $1\%$ નો વઘારો થાય છે. તો કોણીય ઝડપView Solution
- 3દોરી ધરાવતી એક ગરગડીને છત પર નીપત કરેલી છે તેના બંને છેડા આગળ $m $ અને $3m$ દળના પદાર્થ જોડેલો છે. જો ગરગડી અને દોરીનું વજન અવગણ્ય છે અને તે ઘર્ષણ રહીત છે તંત્રનું દ્રવ્યમાન કેન્દ્રનો પ્રવેગ કેટલો હશે ?View Solution
- 4View Solutionકોણીય વેગ સદીશ કઈ દિશામાં હોય?
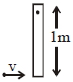
- 5$0.9\, kg$ દળ અને $1 \,m$ લંબાઈ ધરાવતા સળિયાના એક છેડાને અનુલક્ષીને ભ્રમણ કરી શકે છે, $0.1\, kg$ દળ અને $80\,m / s$ના વેગથી આવતો કણ નીચેના છેડે ચોંટી જતા કોણીય ઝડપ .......View Solution
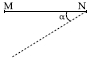
- 6એક પાતળા સળિયા $MN$ ના છેડા $N$ ને સમક્ષિતિજમાં એવી રીતે જોડેલો છે કે જેથી તે શિરોલંબ સમતલમાં મુક્ત રીતે ફરી શકે. જ્યારે સળિયો સમક્ષિતિજ સાથે $\alpha $ નો ખૂણો બનાવે ત્યારે તેને મુક્ત કરવામાં આવે છે તો ત્યારે છેડા $M$ નો વેગ કેટલો હશે?View Solution
- 7એક $W$ વજન ધરાવતા સળિયાને સમક્ષિતિજ સ્થિતિમાં સમતોલનમાં રહેલ બે તીક્ષ્ણ ધારો $A$ અને $B$ પર સમાંતરામાં મૂકેલ છે. તીક્ષ્ણ ધારો વચ્ચેનું એકબીજાથી અંતર $d$ છે. $A$ ધારથી સળિયાનું દ્રવ્યમાન કેન્દ્ર $x$ અંતરે છે. $A$ પરનું લંબબળ કેટલું હશે?View Solution
- 8સમાન પ્રકારના બે કણો એકબીજા તરફ અનુક્રમે $2v$ અને $v$ વેગથી ગતિ કરે છે. આ તંત્રના દ્રવ્યમાન-કેન્દ્રનો વેગ.......View Solution
- 9કેન્દ્રમાંથી પસાર થતી અને લંબાઈને લંબરૂપે રહેલ અક્ષને અનુલક્ષીને એક નળાકારીય સળિયાની ચક્રાવર્તન ત્રિજ્યા $(radius\,of\,gyration) \dots \dots m$ હશે. (સળિયાની લંબાઈ $10 \sqrt{3} m$ આપેલ છે).View Solution
- 10કોઈ પદાર્થ પર ટોર્ક લગાવ્યા વગર, પરંતુ જડત્વની ચાકમાત્રા માં ફેરફાર થવાથી તેની કોણીય ઝડપ ${\omega _1}$ માથી ${\omega _2}$ થાય છે. તો બંને કિસ્સામાં ચક્રાવર્તનની ત્રિજ્યાનો ગુણોત્તર શું થશે?View Solution
