$3mm$ જાડાઇ અને $6cm$ વ્યાસ ધરાવતા સમતલ બર્હિગોળ લેન્સમાં પ્રકાશની ઝડપ $ 2\times 10^8 m/sec$ હોય,તો તેની કેન્દ્રલંબાઇ કેટલા ......$cm$ હશે.
JEE MAIN 2021,JEE MAIN 2013, Diffcult
c
(c) According to lens formula \(\frac{1}{f} = (\mu - 1)\left[ {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right]\)
(c) According to lens formula \(\frac{1}{f} = (\mu - 1)\left[ {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right]\)
The lens is plano-convex i.e., \({R_1} = R\) and \({R_2} = \infty \)
Hence \(\frac{1}{f} = \frac{{\mu - 1}}{R} \Rightarrow f = \frac{R}{{\mu - 1}}\)
Speed of light in medium of lens \(v = 2 \times {10^8}\) \(m/s\)
==> \(\mu = \frac{c}{v} = \frac{{3 \times {{10}^8}}}{{2 \times {{10}^8}}} = \frac{3}{2} = 1.5\)
If \(r\) is the radius and \(y\) is the thickness of lens (at the centre), the radius of curvature \(R\) of its curved surface in accordance with the figure is given by
\({R^2} = {r^2} + {(R - y)^2} \Rightarrow {r^2} + {y^2} - 2Ry = 0\)
Neglecting \({y^2};\) we get \(R = \frac{{{r^2}}}{{2y}} = \frac{{{{(6/2)}^2}}}{{2 \times 0.3}} = 15 cm\)
Hence \(f = \frac{{15}}{{1.5 - 1}} = 30 cm\)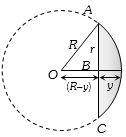
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વસ્તુને પડદાથી $1.50\, m$ અંતરે મૂકેલ છે અને બહિર્ગોળ અરીસાને વચ્ચે મૂકવામાં આવતાં પડદા પર ચાર ગણું મોટું પ્રતિબિંબ ઉદ્દભવે છે. તો લેન્સની કેન્દ્રલંબાઈ .....$cm$ હશે.View Solution
- 2સંયુક્ત માઇક્રોસ્કોપ માટે મોટવણી $375$ અને ટ્યૂબલંબાઈ $150\; \mathrm{mm}$ અને ઓબ્જેક્ટિવ લેન્સની કેન્દ્રલંબાઈ $5\; \mathrm{mm}$ હોય તો નેત્રકાચની કેન્દ્રલંબાઈ કેટલા .....$mm$ રાખવી જોઈએ?View Solution
- 3$6 cm$ જાડાઇ ધરાવતો કાંચનો સ્લેબની એક સપાટી પર ચાંદી લગાવેલ છે. પ્રથમ સપાટીથી $8cm$ અંતરે મૂકેલી વસ્તુનું પ્રતિબિંબ ચાંદી લગાવેલી સપાટીની પાછળ $12cm$ અંતરે મળે છે. તો કાંચનો વક્રીભવનાંક કેટલો હશે?View Solution
- 4$\sqrt{7} \,m$ ઊંડાઈ સુધી પાણી ભરેલી ટાંકીના તળિયા આગળ એક નાનો બલ્બ મૂકેલ છે. પાણીનો વક્રીભવનાંક $\frac{4}{3}$ છે. બલ્બમાં નીકળતો પ્રકાશ પાણીનાં ભાગમાંથી બહાર (નિર્ગમન) આવતો હોય તે ભાગનું ક્ષેત્રફળ $x \pi m^{2}$ છે. $x$ નું મૂલ્ય ............ થશે.View Solution
- 5View Solutionસંયુક્ત સૂક્ષ્મદર્શક યંત્રમાં મધ્યસ્થી પ્રતિબિંબ સામાન્ય રીતે .......હોય છે.
- 6View Solutionજ્યારે પાતળા બહિર્ગોળ લેન્સ ને તેટલી જ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાના સંપર્કમાં મૂકવામાં આવે છે. તંત્રની પરિણામી કેન્દ્રલંબાઈ ......છે.
- 7એસ્ટ્રોનોમિકલ ટેલિસ્કોપમાં ઓબ્જિેકિટવપીસ અને આઇપીસ ની કેન્દ્રલંબાઇ $60cm$ અને $10cm$ છે. તો મોટવણી કેટલી થાય?View Solution
- 8View Solutionજ્યારે પ્રકાશના કિરણપૂંજ ને સમતલ અરીસા પર આપાત કરવામાં આવે છે, ત્યારે તે વાસ્તવિક પ્રતિબિંબ રચે છે. તો આપાત કિરણપૂંજ કેવું હોવું જોઈએ ?
- 9આંખના ડોકટરે $40cm$ કેન્દ્રલંબાઇ ધરાવતા બર્હિગોળ લેન્સ અને $25 cm$ કેન્દ્રલંબાઇ ધરાવતા અંર્તગોળ લેન્સ સંપર્કમાં રાખીને પહેરવાનું કહે છે.તો તેના લેન્સનો પાવર કેટલો થાય?View Solution
- 10માધ્યમ માટે વક્રીભૂતકોણ $(sin r)$ અને આપાતકોણ($sin i)$ નો આલેખ આપેલ છે,જો માધ્યમમાં પ્રકાશની ઝડપ $nc$ હોય,તો $n=$ ____View Solution