$4 \,{amu}$ અને $16\, amu$ દળ ધરાવતા બે આયન પરના વિદ્યુતભાર અનુક્રમે $+2 {e}$ અને $+3 {e}$ છે. આ આયનો સતત લંબરૂપ ચુંબકીય ક્ષેત્ર ધરાવતા પ્રદેશમાંથી પસાર થાય છે. જો બંને આયનની ગતિઉર્જા સમાન હોય તો ....
JEE MAIN 2021, Diffcult
b
\({r}=\frac{{P}}{{qB}}=\frac{\sqrt{2 {mk}}}{{qB}}\)
\({r}=\frac{{P}}{{qB}}=\frac{\sqrt{2 {mk}}}{{qB}}\)
Given they have same kinetic energy
\({r} \propto \frac{\sqrt{{m}}}{{q}}\)
\(\frac{{r}_{1}}{{T}_{2}}=\frac{\sqrt{4}}{2} \times \frac{3}{\sqrt{16}}=\frac{3}{4}\)
\({I}_{2}=\frac{4 {r}_{1}}{3}\left[{r}_{2}\right.\) is for hearier ion and \({r}_{1}\) is for lighter ion)
\(\sin \theta=\frac{{d}}{{R}}\)
\(\theta \rightarrow\) Deflection
\(\theta \propto \frac{1}{{R}}\)
\(({R} \rightarrow\) Radius of path)
\(\because {R}_{2}>{R}_{1} \Rightarrow \theta_{2}<\theta_{1}\)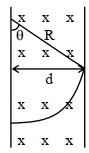
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઅનિયમિત આકારની લૂપમાં પ્રવાહ પસાર કરીને ચુંબકીય ક્ષેત્રમાં મૂકવાથી ..... .
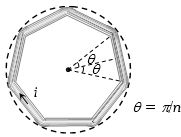
- 2$n$ બાજુવાળા બહુકોણની ત્રિજયા $a$ છે,તો કેન્દ્ર $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 3પ્રવાહ ધારિત વર્તુળાકાર ગાળાનાં કેન્દ્ર આગળ યુંબકીય ક્ષેત્ર $B _1$ છે. આપેલ ગાળાના કેન્દ્રથી તેની ત્રિજ્યા કરતા $\sqrt{3}$ ગણા અંતરે તેની અક્ષ ઉપર ચુંબકીય ક્ષેત્રની $B _2$ છે. $B _1$ અને $B _2$ ગુણોત્તર $B _1 / B _2................$ થશે.View Solution
- 4$16\times10^{-16}\, C$ વિજભાર ધરાવતો કણ $10\, ms^{-1}$ ના વેગથી $x-$ દિશામાં એક ક્ષેત્રમાં દાખલ થાય છે. જ્યાં ચુંબકીય ક્ષેત્ર $\vec B$ એ $y-$ દિશામાં અને $10^4\, Vm^{-1}$ મૂલ્યનું વિદ્યુતક્ષેત્ર $z-$દિશામાં પ્રવર્તે છે. જો કણ $x-$દિશામાં ગતિ કરવાનું શરૂ રાખે તો ચુંબકીયક્ષેત્ર $\vec B$ નું મૂલ્ય કેટલું હશે?View Solution
- 5કોઈ વિસ્તારમાં ચુંબકીય ક્ષેત્ર $\vec{B}=B_0\left(1+\frac{x}{l}\right) \hat{k}$ અસ્તિત્વ ધરાવે છે.$l$ બાજુની અને $i$ વિદ્યુતપ્રવાહ ધરાવતી એક ચોરસ રીંગ તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે.રીંગ વડે અનુભવતા કુલ ચુંબકીય બળની માત્રા શોધો.View Solution
- 6એક emf $90\,V$ ની બેટરીને $100\,\Omega$ ના બે આવરોધોના શ્રેણી જોડાણ સાથે લગાડેલ છે. $400\,\Omega$ આંતરિક અવરોધનું એક વોલ્ટમીટર પ્રત્યેક અવરોધના છેડા વચ્ચે સ્થિતિમાન તફાવત માપવા માટે વપરાય છે. તો વોલ્ટ મીટરનું આવલોકન $.........$ હોય.View Solution
- 7$1 \,MeV$ ની ઊર્જા ધરાવતો પ્રોટોન નિયમિત ચુંબકીયક્ષેત્રમાં $R$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ગતિ કરે છે. $\alpha$ કણની ઉર્જા .......$MeV$ હોવી જોઈએ કે જેથી તે સમાન ત્રિજ્યાના પથમાં સમાન ક્ષેત્રમાં આગળ વધી શકે?View Solution
- 8$8 \,\Omega $ અવરોઘ ધરાવતા ગેલ્વેનોમીટરને $2 \, \Omega $ શંટ જોડેલ છે,તો કુલ પ્રવાહ $1 \, amp$ માંથી કેટલા .............. $amp$ પ્રવાહ શંટમાંથી પસાર થાય?View Solution
- 9$5\,cm$ ત્રિજ્યા ધરાવતા અને એકદદમ નજીક-નજીક વીંટળાયેલા વર્તુળાકાર ગૂંચળા (ગાળા) ને કારણે તેના કેન્દ્ર આગળ $37.68 \times 10^{-4}\,T$ જેટલું ચુંબકીયક્ષેત્ર ઉત્પન્ન થાય છે. ગૂંચળાંમાંથી વહેતો પ્રવાહ $..........\;A$ છે. [ધારો કે આંટાની સંખ્યા $100$ છે અને $\pi=3.14$ ]View Solution
- 10એક વિદ્યુતભારિત કણ નિયમિત ચુંબકીય ક્ષેત્રમાં વર્તુળાકાર માર્ગ પર ગતિ કરે છે. વિદ્યુતભારિત કણની ગતિઊર્જા તેના પ્રારંભિક મૂલ્ય કરતાં $4$ ઘણી વધે છે. તેના વિદ્યુતભારિત કણના વર્તુળાકાર પથની નવી ત્રિજયા અને મૂળ ત્રિજ્યાનો ગુણોત્તર ............ થશે.View Solution
