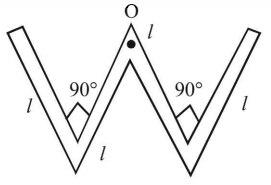
$4\,l$ લંબાઈ અને $4\,m$ દળ ધરાવતો પાતળો સળિયો આકૃતિ મુજબ વાળવામાં આવે છે. તેના સમતલને લંબ અને $O$ માંથી પસા થતી $axis$ આગળ તેની જડત્વની ચાકમાત્રા $.......$

Medium
b
(b)
(b)
Total moment of inertia
\(= I _1+ I _2+ I _3+ I _4=2 I _1+2 I _2\)
\(=2\left( I _1+ l _2\right)\left[ I _3= I _1, I _1= I _4\right]\)Now, \(I _2= I _3=\frac{ Ml ^2}{3}\)
Using parallel axes theorem, we have
\(I = I _{ CM }+ Mx ^2 \text { and } x =\sqrt{l^2+\frac{l^2}{4}}\)
\(I _1= I _4=\frac{ M l^2}{12}+ M \left[\sqrt{l^2+\left(\frac{l}{2}\right)^2}\right]^2\)
Putting all values we get
Moment of inertia, \(I =10\left(\frac{ Ml ^2}{3}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ ધરાવતો પદાર્થ $A$ ગુરુત્વાકર્ષણ બળની અસર હેઠળ પડતાં તે બે ટુકડાઓમાં વિભાજિત થાય છે. એક ટુકડો $B$ નું દળ $1/3\ M$ અને બીજા ટુકડા $ C$ નું દળ $ 2/3\ M$ છે. પદાર્થ $A$ ના દ્રવ્યમાન કેન્દ્રની સાપેક્ષે ટુકડાઓ $ B$ અને $ C$ થી બનતાં તંત્રનું દ્રવ્યમાન-કેન્દ્ર .....View Solution
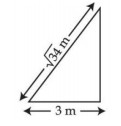
- 2$\sqrt{34} \,m$ લાંબી અને $10 \,kg$ વજન ધરાવતી એક સીડી (નીસરણી) ધર્ષણરહિત દિવાલ પર ટેક્વેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે તેના પગ (નીચેનો છેડો) દિવાલથી $3 \,m$ અંતરે રાખેલ છે. જો $F _{f}$ અને $F _{ w }$ એ અનુક્રમે ભોંયતળિયા અને દિવાલ દ્વારા લાગતું લંબબળ હોય તો ગુણોત્તર $F _{ w } / F _{f}$ ............ થશે.View Solution
$\left(g=10 \,m / s ^{2}\right.$ નો ઉપયોગ કરો.)
- 3$m$ દળનો એક પત્થર કોઈ દોરીના છેડે બાંધીને એક સમક્ષિતિજ ઘર્ષણરહિત ટેબલ પર વર્તુળાકારે ફેરવવામાં આવે છે. પત્થરનું કોણીય વેગમાન વર્તુળના કેન્દ્રને અનુલક્ષીને અચળ રહે તેમ દોરીની લંબાઈ ધીમે ધીમે ઘટાડવામાં આવે છે. દોરીનું તણાવ $T\, = Ar^n$ (જ્યાં $A$ એ અચળાંક છે) દ્વારા આપેલ છે, એ વર્તુળની તત્કાલિન ત્રિજ્યા છે. તો $n$ ની કિંમત શું હશે?View Solution
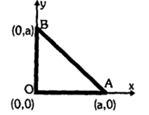
- 4View Solutionત્રણ સમાન દળના સળિયા આકૃતિમાં દર્શાવેલ છે. તંત્રના દ્રવ્યમાન કેન્દ્રના યામાક્ષ બિંદુઓ શોધો.
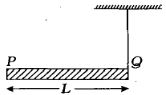
- 5$M $ દળ અને $L$ લંબાઈ ધરાવતા એક સળિયા $PQ$ નો $P$ છેડો જડિત કરેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે, દળ રહિત દોરી વડે બિંદુ $Q$ સાથે બાંધીને આ સળિયાને સમક્ષિતિજ રાખવામાં આવેલ છે. જયારે દોરીને કાપી નાખવામાં આવે, ત્યારે સળિયાનો પ્રારંભિક કોણીય પ્રવેગ કેટલો થશે?View Solution
- 6View Solutionએક પ્રયોગમાં એક જેટ એંજિનનું કમ્પ્રેસર નીચે આપેલા ગ્રાફ પ્રમાણે ફરે છે તો પ્રયોગ દરમિયાન કમ્પ્રેસરના પરિભ્રમણ સંખ્યા કેટલી હોય ?
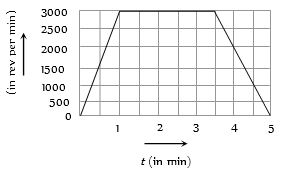
- 7દળ તથા $ R $ ત્રિજ્યાવાળા ચાર નક્કર ગોળાઓ એક ચોરસના ચાર ખૂણાઓ પર મૂકેલા છે. જો ચોરસની બાજુનું માપ $ 'a'$ હોય, તો ચોરસની કોઈ એક બાજુને અક્ષ તરીકે લેતાં, તેને અનુલક્ષીને આ તંત્રની જડત્વની ચાકમાત્રા શોધો.View Solution
- 8દોરી ધરાવતી એક ગરગડીને છત પર નીપત કરેલી છે તેના બંને છેડા આગળ $m $ અને $3m$ દળના પદાર્થ જોડેલો છે. જો ગરગડી અને દોરીનું વજન અવગણ્ય છે અને તે ઘર્ષણ રહીત છે તંત્રનું દ્રવ્યમાન કેન્દ્રનો પ્રવેગ કેટલો હશે ?View Solution
- 9$R$ ત્રિજયા અને $M$ દળ ધરાવતી એક નિયમિત વર્તુળાકાર તકતીને લંબ એવી રીતે તેની ધારમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 10એક પૈડું $900\, rpm$ ની કોણીય ઝડપથી ભ્રમણ કરે છે.તે $1$ મિનિટમાં સ્થિર થઇ જતું હોય,તો કોણીય પ્રતિપ્રવેગ $radian/$$s^2$માં કેટલો થાય?View Solution
