$500\,cm^2$ ક્ષેત્રફળ અને $1000$ આંટા ધરાવતી કોઇલ પર ચુંબકીય ક્ષેત્ર લંબ લાગે છે,ચુંબકીયક્ષેત્ર $ 2 \times {10^{ - 5}}\,Wb/{m^2} $ હોય,તો કોઇલને $0.2\, sec$ માં $ {180^o} $ ફેરવતાં કેટલો $emf$ ($mV$ માં) ઉત્પન્ન થાય?
Medium
Download our app for free and get started
b
(b) By using \(e = - \frac{{NBA\left( {\cos {\theta _2} - \cos {\theta _1}} \right)}}{{\Delta t}}\)
(b) By using \(e = - \frac{{NBA\left( {\cos {\theta _2} - \cos {\theta _1}} \right)}}{{\Delta t}}\)
\(e = - \frac{{1000 \times 2 \times {{10}^{ - 5}} \times 500 \times {{10}^{ - 4}}\left( {\cos {{180}^o} - \cos {0^o}} \right)}}{{0.2}}\)
\( = {10^{ - 2}}volt = 10\,mV\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2\,cm ^2$ નું વર્તુળાકાર આડછેદનું ક્ષેત્રફળ ધરાવતો અને $40\,cm$ ની લંબાઈ ધરાવતા એક સળિયા ઉપર, એક અવાહક પડ ચઢાવેલા તાર વડે નિયમિત $400$ આંટા સાથે વીટાળવામાં આવેલ છે. જો વીટાળેલા તારમાંથી $0.4\,A$ નો પ્રવાહ પસાર થતો હોય, તો આટાંઓની અંદર ઉત્પન્ન થતું પરિણામી ચુંબકીય ફલકસ $4 \pi \times 10^{-6}\,Wb$ મળે છે. સળિયાની સાપેક્ષ પારગમ્યતા $...........$ થશે.(શૂન્યાવકાશની પારગમ્યતા $\mu_0=4 \pi \times 10^{-7}\,NA ^{-2}$ આપેલ છે.)View Solution
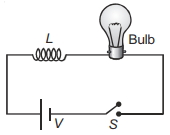
- 2View Solutionઆપેલ આકૃતિ માટે બલ્બ ક્યારે અચાનક પ્રકાશીત થશે
- 3એક સુવાહક વર્તુળાકાર ગાળાને $\overrightarrow{ B }=\left(3 t ^3 \hat{ j }+3 t ^2 \hat{k}\right)- SI$ એકમમાં જેટલા ચુંબકીય ક્ષેત્રમાં $X- Y$ સમતલમાં મૂકવામાં આવેલ છે. ને ગાળાની ત્રિજ્યા $1\,m$ હોય, $t =2$ સેકન્ડે ગાળામાં પ્રેરિત $emf\,n \pi\,V$ છે. તો $n$ ની કિંમત હશે.View Solution
- 4View Solutionઆદર્શ સ્ટેપ ડાઉન ટ્રાન્સફોર્મરમાં શેનું મૂલ્ય વધે છે?
- 5નાની લંબાઈ $L$ તથા $A$ આડછેદ ધરાવતાં સોલેનોઈડમાં સંગ્રહ પામતી ચુંબકીય ઊર્જાView Solution
- 6View Solutionવિદ્યુત મોટર શું કાર્ય કરે?
- 7View Solutionએક કોઈલનો નિયમિત ચુંબકીય ક્ષેત્રમાં એવી રીતે લટકાવેલ છે જેથી કોઈલનું સમતલ એ બળની ચુંબકીય રેખાઓ સાથે સમાંતર રહે. જ્યારે કોઈલમાંથી પ્રવાહ પસાર કરવામાં આવે છે ત્યારે તે દોલનો કરે છે. તેને રોકવા ખૂબ મુશ્કેલ છે. પણ જો એલ્યુમિનિયમ પ્લેટને કોઈલની નજીક રાખવામાં આવે તો, તે રોકાઈ જાય છે. તેનુ કારણ
- 8$1\, {m}$ ત્રિજ્યા ધરાવતા વર્તુળાકાર વાહક ગુંચળાને ચુંબકીય ક્ષેત્ર $\vec {B}$ ના ફેરફાર દ્વારા ગરમ કરવામાં આવે છે, જ્યાં ચુંબકીય ક્ષેત્ર ગૂચાળાના સમતલને લંબ પસાર થાય છે. ગુંચળાનો અવરોધ $2\, \mu\, \Omega$ છે. ચુંબકીય ક્ષેત્ર ધીમે ધીમે એવી રીતે બંધ થાય છે કે જેથી તેનો સમય સાથેનો ફેરફાર $B =\frac{4}{\pi} \times 10^{-3} T \left(1-\frac{ t }{100}\right)$ મુજબનો છે. ચુંબકીયક્ષેત્ર સંપૂર્ણપણે બંધ થાય તે પહેલાં ગુંચળા દ્વારા વિખરાયેલી ઊર્જા $E$ ($m \,J$ માં) કેટલી હશે?View Solution
- 9એક $A.C.$ જનરેટરમાં સમાન ક્ષેત્રફળ $A$ ધરાવતા $N$ આંટાઓ વાળું ગુચળું, જેમનો કુલ અવરોધ $R$ છે અને તે યુંબકીયક્ષેત્ર $B$ માં $\omega$ આવૃત્તિથી પરિભ્રમણ કરે છે, તો ગુંચળા દ્રારા ઉત્પન થતો મહત્તમ $emf$ કેટલો હશે?View Solution
- 10$0.2\; m$ ત્રિજયાની વર્તુળાકાર તકતીને $\frac{1}{\pi }\;Wb/m^2$ મૂલ્યના નિયમિત ચુંબકીયક્ષેત્રમાં એવી રીતે મૂકેલી છે કે તેની અક્ષ $\vec B$ સાથે $60^o$ નો કોણ બનાવે છે. તકતી સાથે સંકળાયેલ ફ્લકસ ($Wb$ માં) કેટલું હશે?View Solution