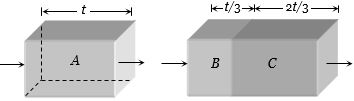
$A$ અને $C $ નો વક્રીભવનાંક $1.5 $ અને $1.6 $ છે. $B$ અને $C$ ની જાડાઇનો ગુણોત્તર $1:2$ છે.બંને પર કિરણ આપાત કરતાં બંને બ્લોકમાં તરંગોની સંખ્યા સમાન હોય, તો $B$ નો વક્રીભવનાંક કેટલો હશે?
Medium
Download our app for free and get started
c
(c) For \(A\)
(c) For \(A\)
Total number of waves = \(\frac{{(1.5)t}}{\lambda }\) ....\((i)\)
\(\because\) \(\left(\begin{array}{l}{\rm{Total\,number}}\\\;\;{\rm{ \,of\, waves}}\end{array} \right) = \left({\frac{{{\rm{optical \,path \,length}}}}{{{\rm{wavelength}}}}} \right)\)
For \(B\) and \(C\)
Total number of waves = \(\frac{{{n_B}\left({\frac{t}{3}} \right)}}{\lambda } + \frac{{(1.6)\left({\frac{{2t}}{3}} \right)}}{\lambda }\) ....\((ii)\)
Equating \((i)\) and \((ii)\) \({n_B} = 1.3\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક તરવૈયો પાણીની અંદરથી બહારની બાજુ વર્તુળાકાર ક્ષેત્રમાં જોવે છે. પાણીનો વક્રીભવનાંક $\frac{4}{3}$ અને તરવૈયાની આંખ પાણીની સપાટીથી $15\, cm$ ઊંડાઈએ છે. તો તેને બહાર દેખાતા ક્ષેત્રના વર્તુળની ત્રિજ્યા કેટલી હશે?View Solution
- 2$10\,\,cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સના પ્રથમ કેન્દ્રબિંદુથી $5\,\, cm $ અંતરે પદાર્થ મૂક્લો છે. જો વાસ્તવિક પ્રતિબિંબ રચાતુ હોય તો તેનું લેન્સથી અંતર ........$cm$ છે.View Solution
- 3સમતલ બહિર્ગોળ કાચના લેન્સની કેન્દ્રલંબાઈ $20\, cm \left(\mu_{ g }\right. =1.5)$ છે. તેની સમતલ સપાટી પર ચાંદીનો ઢોળ ચડાવવામાં આવે છે. એક પ્રકાશીત વસ્તુને લેન્સથી $60\, cm$ અંતરે તેની અक्ष પર બહિર્ગોળ બાજુએ મૂકવામાં આવે છે. તો પ્રતિબિંબનું અંતર ($cm$ માં) કેટલું છે ?View Solution
- 4$2000 \,\,m$ ઉંચાઈએ ઉડી રહેલા વિમાન દ્વારા જમીન પરનો ફોટોગ્રાફ $ 50\,\, cm$ કેન્દ્રલંબાઈના લેન્સ ધરાવતા કેમેરા વડે લેવામાં આવે છે. કેમેરામાં ફીલ્મનું કદ $18\,\, cm × 18\,\, cm$ છે. કોઈ એક સમયે આ કેમેરા વડે ફોટોગ્રાફ પાડી શકાતા સપાટીનું ક્ષેત્રફળ કેટલું હશે?View Solution
- 5એક સમતલ બર્હિગોળ લેન્સ એ એક સમતલ અંતર્ગોળ લેન્સમાં બરોબર બેસે છે. બંનેની સમતલ સપાટી એકબીજાને સમાંતર છે. જો લેન્સ ${\mu _1}$ અને${\mu _2}$ વક્રીભવનાંકવાળા ભિન્ન પદાર્થોના બનેલા હોય તથા તેમની વક્ર સપાટીની વક્રતા ત્રિજયા $R$ હોય, તો આવા સંયુકત લેન્સની કેન્દ્રલંબાઈ કેટલી થાય?View Solution
- 6$n$ વક્રીભવનાંકવાળા પારદર્શક માઘ્યમમાં એક પ્રકાશકિરણ ગતિ કરતું કરતું હવા અને માઘ્યમને છૂટી પાડતી સંપર્ક સપાટી પાસે આપાતબિંદુએ $45^o $ જેટલા આપાતકોણે આપાત થાય છે,તો વક્રીભવનાંક $n$ ના કયા મૂલ્ય માટે આ કિરણનું પૂર્ણ આંતરિક પરાવર્તન થશે?View Solution
- 7View Solutionસાદા માઇક્રોસ્કોપમાં માણસને પ્રતિબિંબ કેવું દેખાશે.
- 8$10\,\,cm$ કેન્દ્રલંબાઈ ધરાવતાં અપસારી લેન્સથી એક બિંદુવત ઉદ્દગમને $15\,\,cm$ ના અંતરે મૂકેલો છે. $12\,\, cm$ કેન્દ્રલંબાઈનાં અંત:ર્ગોળ અરીસાને .......$cm$ મૂકેલ હોવો જોઈએ કે જેથી તેની જાતે વસ્તુ પર વાસ્તવિક પ્રતિબિંબ રચાયેલું હોય?View Solution
- 9$60^o $ નો પ્રિઝમકોણ ધરાવતા પ્રિઝમ માટે લઘુત્તમ વિચલનકોણ $30^o$ હોય,તો આપાતકોણ કેટલા .....$^o$ હશે?View Solution
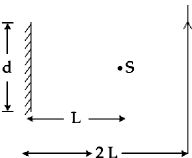
- 10એક દિવાલ પર શિરોલંબ લટકાવેલ $d$ પહોળાઇના એક સપાટ અરિસાના કેન્દ્રની સામે $L$ અંતર પર પ્રકાશનો એક બિંદુવત ઉદગમ $S$ મુકેલ છે. આ અરિસાથી $2L$ અંતરે એક સમાંતર રેખા પર અરિસાની સામેથી એક માણસ પસાર થાય છે આ માણસને અરિસામાં પ્રકાશના ઉદગમનું પ્રતિબિંબ ક્યા અંતરે દેખાશે ?View Solution
