For two concentric circular coil,
Mutual Inductance \(M=\frac{\mu_{0} \pi \mathrm{N}_{1} \mathrm{N}_{2} \mathrm{a}^{2}}{2 \mathrm{b}}\)
here, \(\mathrm{N}_{1}=\mathrm{N}_{2}=1\)
Hence, \(M=\frac{\mu_{0} \pi a^{2}}{2 b}.........(i)\)
and given \(I=I_{0} \cos \omega t.........(ii)\)
Now according to Faraday's second law induced \(emf\)
\(\mathrm{e}=-\mathrm{M} \frac{\mathrm{d} \mathrm{I}}{\mathrm{dt}}\)
Fromeq. \((ii)\)
\(\mathrm{e}=\frac{-\mu_{0} \pi \mathrm{a}^{2}}{2 \mathrm{b}} \frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{I}_{0} \cos \omega \mathrm{t}\right)\)
\(\mathrm{e}=\frac{\mu_{0} \pi \mathrm{a}^{2}}{2 \mathrm{b}} \mathrm{I}_{0} \sin \omega \mathrm{t}(\omega)\)
\(\mathrm{e}=\frac{\pi \mu_{0} \mathrm{I}_{0}}{2} \cdot \frac{\mathrm{a}^{2}}{\mathrm{b}} \omega \sin \omega \mathrm{t}\)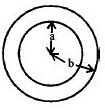
Download our appand get started for free
Similar Questions
- 1નીચે આપેલા વિધાનોમાંથી એક વિધાન $A$ છે અને બીજું વિધાન કારણ $R$ છે.View Solution
વિધાન $A:$ એક ગજિયા ચુંબકને જયારે ધાત્વીત નળાકારમાંથી પસાર કરવામાં આવે છે ત્યારે લાગતો સમય એક અચુંબકીય દંડા કે જે સમાન ભૂમિતિ અને દળ ધરાવે છે તેના કરતાં વધુ હોય છે.
કારણ $R:$ ગજિયા ચુંબક માટે ધાતુની નળીમાં એડી વીજપ્રવાહ ઉત્પન્ન થાય છે, કે જે ગંજિયા ચુંબકની ગતિને અવરોધે છે.
ઉપરોક્ત સત્યાર્થતા ને આધારે, સાચો જવાબ નીચેના વિકલ્પોમાંથી પસંદ કરો.
- 2એક આંટો ધરાવતી $a$ બાજુવાળી ચોરસ લૂપને બીજા $b(b \gg a)$ બાજુવાળી ચોરસ લૂપની અંદર સમકેન્દ્રિય રીતે મુકેલ છે. જો $b$ બાજુવાળી ચોરસ લૂપની અંદર $I$ પ્રવાહ પસાર કરવામાં આવે તો આ બંને લૂપ વચ્ચેનું અન્યોન્ય પ્રેરકત્વ કેટલું થાય?View Solution
- 3$2.0$ હેનરી આત્મપ્રેરણ ધરાવતા ઈન્ડકટરમાં $I =2 \sin \left( t ^{2}\right) A$ એમ્પિયર મુજબ પ્રવાહ વધે છે. જ્યારે પ્રવાહ $0$ થી બદલાઈને $2\,A$ થાય તે ગાળામાં વપરાતી ઊર્જા........$J$ થશે.View Solution
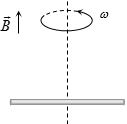
- 4$2l$ લંબાઇના સળિયાને લંબ દ્વિભાજકને અનુલક્ષીને $\omega$ કોણીય ઝડપથી ફેરવવામાં આવે છે,ચુંબકીયક્ષેત્ર $ \overrightarrow B $ અક્ષને સમાંતર છે,તો બે છેડા વચ્ચે કેટલો $emf$ ઉત્પન્ન થાય?View Solution
- 5ટ્રાન્સફોર્મરનો ઉપયોગ $220\,V$ મુખ્યમાંથી $100\,W$ અને $110\,V$ ના બલ્બને પ્રકાશિત કરવામાં આવે છે. જો મુખ્ય પ્રવાહ $0.5\;amp$ હોય, તો ટ્રાન્સફોર્મરની કાર્યક્ષમતા ($\%$ માં) આશરે કેટલી હશે?View Solution
- 6$2\, H$ પ્રેરણ અને અવગણ્ય અવરોધ ધરાવતા એક ગુંચળાને જેનો વોલ્ટેજ $V =3t$ વોલ્ટ થી દર્શાવી શકાય તેવા ઉદ્દગમ સાથે જોડવામાં આવે છે. (જ્યાં, $t$ એ સેકન્ડમાં છે). જ્યારે $t= 0$ સમયે વોલ્ટેજ લગાડવામાં આવે છે ત્યારે $4$ સેકન્ડ બાદ ગુંચળામાં સંગ્રહિત ઊર્જા .............$J$ થશે.View Solution
- 7સ્ટેપ ડાઉન ટ્રાન્સફોર્મર $1000\,V$ પર લગાવતાં $120\,V$ પર $20\,A$ પ્રવાહ સપ્લાય કરે છે,જો ટ્રાન્સફોર્મરની કાર્યક્ષમતા $80\%$ હોય,તો પ્રાથમિક ગૂંચળામાં પ્રવાહ કેટલા .......$A$ હશે?View Solution
- 8એક આદર્શ ટ્રાન્સફોર્મરના પ્રાથમિકમાં $100$ આંટાઓ અને ગૌણમાં $250$ આંટાઓ છે એસી વિદ્યુતસ્થિતિમાનનું મહત્તમ મૂલ્ય $28\; V$ છે તો $r.m.s.$ મૂલ્ય આશરે કેલલંં છે?View Solution
- 9$10\,cm$ ત્રિજ્યા ધરાવતી કોઈલ નું સમતલન $3.0 \times 10^{-5}\, T$ ના ચુબકીયક્ષેત્ર ને લંબ મૂકેલી છે. કોઈલના વ્યાસને અનુલક્ષીને અને ચુબકીયક્ષેત્રને લંબ અક્ષને અચળ કોણીય ઝડપથી ફેરવવામાં આવે છે. $0.2\,Sec$ માં અડધુ પરિભ્રમણ કરે છે. કોઇલમાં ઉદભવતું મહતમ $emf.......\mu V$View Solution
- 10View Solutionટ્રાન્સફોર્મર કયાં સિધ્દ્વાંત પર કાર્ય કરેં છે.
