આકૃતિમાં દર્શાવેલ સાયનોસોડલ વિદ્યુતસ્થિતિમાન તફાવત $V_1$ અવરોધ $R$ પર લગાવતા $W$ દરે ઉષ્મા ઉત્પન્ન કરે છે. જ્યારે આકૃતિમાં દર્શાવ્યામાં પ્રમાણે ચોરસ તરંગના વિદ્યુત સ્થિતિમાન તફાવત $V_2$ ને અવરોધ પર લગાવવામાં આવે, તો ઉષ્મા વ્યયનો દર કેટલો છે ?
Diffcult
Download our app for free and get started
d
(d)
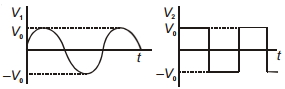
(d)
\(\operatorname{Power}(P)=\frac{V_{ ms }^2}{R}\)
According to the problem
\(w=\frac{\left(\frac{V_0}{\sqrt{2}}\right)^2}{R}\)
for square wave \(V_{ rms }=V_0\)
\(W^{\prime}=\frac{V_0^2}{R}\)
\(\frac{W^{\prime}}{W}=2, \quad W^{\prime}=2\, W\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક શ્રેણી $LCR$ પરિપથને $ac$ વૉલ્ટેજ ઉદગમ સાથે જોડેલ છે જ્યારે પરિપથમાંથી $L$ ને દૂર કરવામાં આવે છે ત્યારે પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $\frac{\pi}{3}$ છે જો તેના બદલે પરિપથમાંથી $C$ ને દૂર કરવામાં આવે ત્યારે ફરીથી પ્રવાહ અને વૉલ્ટેજ વચ્ચેનો કળા તફાવત $\frac{\pi}{3}$ છે આ પરિપથનો શક્તિગુણાંક (power factor) ................. છેView Solution
- 2એક $LC$ દોલકમાં, જો ઈન્ડકટર અને સંધારકનું મૂલ્ય અનુક્રમે બમણું અને આઠગણું કરવામાં આવે તો દોલકની આવૃત્તિ તેની મૂળ પ્રાકૃતિક આવૃત્તિ $\omega_0$ કરતા $x$ નું મુલ્ય $.........$ થશે.View Solution
- 3$300\, {V}$ અને $50 \,{Hz}$ આવૃતિથી ચાલતા $LCR$ શ્રેણી પરિપથમાં અવરોધ ${R}=3 \,{k} \Omega$, ઇન્ડકટરનો રીએકટન્સ $X_{L}=250 \,\pi \Omega$ અને અજ્ઞાત કેપેસીટર છે. જો સરેરાશ પાવરનું મુલ્ય મહતમ કરવું હોય તો કેપેસીટન્સનું મુલ્ય $\mu {F}$ માં કેટલું હોવું જોઈએ? ($\pi^{2}=10$)View Solution
- 4પરિપથમાં પ્રત્યાવર્તી પ્રવાહ અને વોલ્ટેજના તાત્કાલિક મૂલ્યો અનુક્રમે નીચે મુજબ આપવામાં આવે છેView Solution
$ I= \frac{1}{{\sqrt 2 }} sin \left( {100\pi t} \right)$
$E=\frac{1}{\sqrt{2}} \sin (100 \pi t+\pi / 3)$
આ પરિપથમાં થતો સરેરાશ પાવર વ્યય વોટમાં કેટલો હશે?
- 5અનુનાદ વખતે અવરોધ $R$ માંથી પ્રવાહ .... .View Solution
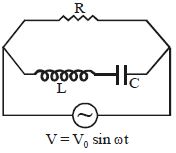
- 6નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન$-I$ : $AC$ પરિપથ વીજ અનુનાદ ત્યારે અનુભવે છે કે જયારે તેમાં સંગ્રાહક કે પ્રેરક આવેલા હોય.
વિધાન$-II$ : $AC$ પરિપથમાં જો શુદ્ધ સંગ્રાહક કે શુદ્ધ પ્રેરક જોડેલા હોય, તો તે શૂન્યેતર પાવર અવયવને લીધે વધુ પાવર ખર્ચાય છે.
ઉપરોક્ત વિધાનોને આધાર,યોગ્ય જવાબ નીચેના વિકલ્પોમાંથી પસંદ કરો.
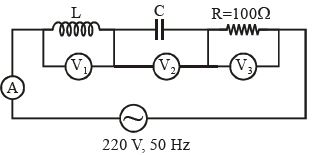
- 7આકૃતિમાં દર્શાવેલ પરિપથમાં વોલ્ટમિટર $V_1$ અને $V_2$ એ $300 \;V $ દર્શાવે છે. વોલ્ટમીટર $V_3$ અને એમિટર $A$ નું રીંડિંગ અનુક્રમે કેટલું થાય?View Solution
- 8કોઈક ક્ષણે એક ઉલટસૂલટ ($ac$) પ્રવાહ નીચે મુજબ આવી શકાયView Solution
$i=[6+\sqrt{56} \sin (100 \pi \mathrm{t}+\pi / 3)] \mathrm{A}$ પ્રવાહનું $rms$ મૂલ્ય. . . . . . .$A$ હશે.
- 9શુદ્ધ (ફકત) અવરોધ ધરાવતા પરિપથ ધટક $X$ને $100\,V$ મહત્તમ વોલ્ટેજ ધરાવતા $a.c.$ ઉદગમ સાથે જોડવામાં આવે છે ત્યારે તે $5A$ નો મહત્તમ પ્રવાહ આપે છે, કે જે વોલ્ટેજ સાથે કળામાં છે. જ્યારે બીજા પરિપથ ધટક $Y$ને આ જ $a.c.$ ઉદગમ સાથે જોડવામાં આવે છે ત્યારે તે પણ સમાન મહત્તમ પ્રવાહ આપે છે. પણ તે કળામાં વોલ્ટેજ કરતાં $\frac{\pi}{2}$ પાછળ છે. જો $X$ અને $Y$ ધટકોને આ જ ઉદગમ સાથે શ્રેણીમાં જોડવામાં આવે છે તો પ્રવાહનું $rms$ મૂલ્ય એમ્પિયરમાં કેટલું હશે ?View Solution
- 10એક શ્રેણી $LCR$ પરિપથમાં $R =8\,\Omega, X _{ L }=100\,\Omega$ અને $X _{ C }=40\,\Omega$ છે.ઈનપુટ વોલ્ટેજ $2500 \cos (100 \pi t )\,V$ છે.પરિપથમાં પ્રવાહનો કંપવિસ્તાર $..............\,A$ થશે.View Solution