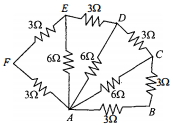
Resistances \(R _{ AF }\) and \(R _{ FE }\) are in series combination. Therefore their equivalent resistance \(R = R _{ AF }+ R _{ FE }=3+3=6 \Omega\). Now the resistance \(R _{ AE }\) and equivalent resistance \(R\) ' are in parallel combination. Therefore relation for their equivalent resistance.
\(\frac{1}{R^{*}}=\frac{1}{R^{\prime}}+\frac{1}{R_{A E}}=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3} \Rightarrow R^{\prime \prime}=3 \Omega\).
We can calculate in the same manner for \(R_{E D}, R_{A C}, R_{D C}\). etc. and finally the circuit
reduces as shown in the figure.
Therefore, the equivalent resistance between \(A\) and \(B\)
\(=\frac{(3+3) \times 3}{(3+3)+3}=\frac{18}{9}=2 \Omega\)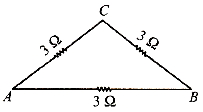
Download our appand get started for free
Similar Questions
- 1View Solutionએક પ્રયોગમા અવરોધને તાપમાનના વિધેય તરીકે નીચે મુજબ સીધી રેખા જેવો આલેખ મળે છે.તો નીચેનામાથી શું સાચું હશે?
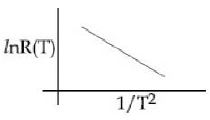
- 2View Solutionફ્યુજમાં વપરાતો તારની લાક્ષણિકતા કેવી હોવી જોઈએ?
- 3$60\,W, 230V$ નો લેમ્પ $8$ કલાક વાપરવામાં આવે છે.$1$ યુનિટના ભાવ $1.25$ રૂપિયા હોય તો કેટલા ............. રૂપિયા બીલ આવશે?View Solution
- 4એક અજ્ઞાત અવરોધમાંથી $2 \,mA$ પ્રવાહ પસાર કરતા તે $4.4 \,W$ પાવર વિખેરિત કરે છે. જ્યારે તેને $11 \,V$ ના આદર્શ પાવર સપ્લાય સાથે જોડવામાં આવે ત્યારે વિખેરિત થતો પાવર ______ હશે.View Solution
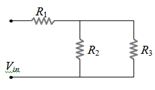
- 5View Solutionઆકૃતિમાં દર્શાવેલ ત્રણે અવરોધમાંથી સમાન ઉષ્મા ઉર્જા ઉત્પન્ન કરવા માટે તેમની કિંમત વચ્ચેનો સંબંધ કયો હોવો જોઈએ ?
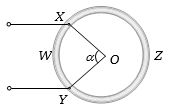
- 6$R$ અવરોધ ધરાવતા વાયરને વાળીને ત્રિજ્યાવાળી વર્તૂળાકાર રીંગ બનાવવામાં આવે છે. તેના પરીઘ પરના બે બિંદુઓ $X$ અને $Y$ વચ્ચેનો પરિણામી અવરોધ શોધો. (ખૂણો $XOY = \alpha$ આપેલ છે.)View Solution
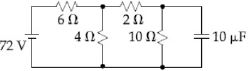
- 7આપેલ પરિપથમાં કેપેસીટર પર કેટલા ............... $\mu C$ વિજભાર હશે?View Solution
- 8$100\,W,200\,V$ ના બલ્બને $100\,V$ સાથે જોડતાં બલ્બમાંથી કેટલો પ્રવાહ પસાર થાય?View Solution
- 9'Incandescent' બલ્બના ફિલામેન્ટનો અવરોધ તાપમાન વધતા વધે છે. જો રૂમના તાપમાને $100\ W, 60\ W$ અને $40\ W$ ના બલ્બના અવરોધ $R_{100}, R_{60}$ અને $R_{40}$ હોય તો...View Solution
- 10નીચે બે વિધાન આપેલ છે .View Solution
વિધાન $I:$ $80\; \Omega$ અવરોધ ધરાવતા એક નિયમિત તારને ચાર સમાન ભાગમાં કાપવામાં આવે છે. આ ભાગોને હવે સમાંતરમાં જોડવામાં આવે છે. આ સંયોજની સમતુલ્ય અવરોધ $5 \Omega$ હશે.
વિધાન $II$: બે અવરોધો $2R$ અને $3R$ ને વિદ્યુત પરિપથમાં સમાંતરમાં જોડવામાં આવે છે. $3R$ અને $2R$ માં ઉત્પન્ન થતી ઉષ્મીય ઊર્જાનો ગુણોત્તર $3: 2$ હશે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
