આકૃતિમાં દર્શાવ્યા પ્રમાણે અનંત પરિપથને $9\, V$ અને $0.5\,\Omega $ આંતરિક અવરોધ ધરાવતી બેટરી સાથે જોડેલ છે. બધા એમીટર $A_1 , A_2, A_3$ અને વોલ્ટમીટર $V$ આદર્શ હોય તો નીચેનામાંથી શું સાચું પડે?
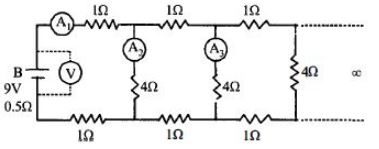

JEE MAIN 2017, Diffcult
a
The given circuit can be redrawn as,
The given circuit can be redrawn as,
as \(4\, \Omega\) and \(x\, \Omega\) are parallel
\(x^{\prime}=\frac{1}{4}+\frac{1}{x}=\frac{(4+x)}{4 x} \quad x^{\prime}=\frac{4 x}{4+x}\)
and \( 1 \,\Omega\) and \(1\, \Omega\) are also in series \(x^{\prime \prime}=2 \,\Omega\) Now equivalent resistance of circuit
\(x=\frac{4 x}{4+x}+2=\frac{8+6 x}{4+x}\)
\(4 x+x^{2}=8+6 x\)
\(x^{2}-2 x-8=0\)
\(x=\frac{2 \pm \sqrt{4-4(1)(-8)}}{2}=\frac{2 \pm \sqrt{36}}{2}\)
\(=\frac{2 \pm 6}{2}=4\, \Omega\)
Reading of Ammeter \(A_{1}=\frac{V}{(R+r)}\)
\(A_{1}=\frac{9}{4+0.5}=2\) \(Ampere\)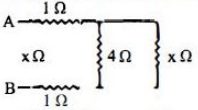
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
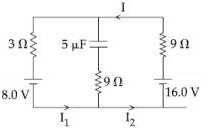
- 1આપેલ પરિપથમાં બે $8.0\,V$ અને $16.0\,V$ ની બેટરી, ત્રણ $3\,\Omega ,\,9\,\Omega $ અને $9\,\Omega $ ના અવરોધો અને $5.0\,\mu F.$ નું કેપેસીટર છે.તો પરિપથમાં સ્થાયી સ્થિતિમાં કેટલા ............. $A$ પ્રવાહ $I$ નું વહન થતું હશે?View Solution
- 2$l$ લંબાઈના અને $d$ વ્યાસ ધરાવતા આઠ કોપરના તારેને જોડીને $R$ અવરોધ ધરાવતો એક સંયુક્ત વાહક બનાવવામાં આવે છે. જે $2l$ લંબાઈના એક કોપર તારને પણ આટલો જ અવરોધ હોય તો તેનો વ્યાસ $..............d$ થશે.View Solution
- 3એક પોટેન્શિયોમીટરના પ્રયોગમાં કોષ માટે બેલેન્સિંગ લંબાઈ $560 \;\mathrm{cm}$ છે હવે જો $10 \;\Omega$ ના અવરોધને કોષ સાથે સમાંતરમાં જોડતા બેલેન્સિંગ લંબાઈ $60\; \mathrm{cm} $ મળે છે.જો કોષનો આંતરિક અવરોધ $\frac{\mathrm{N}}{10} \;\Omega,$ હોય તો $\mathrm{N}$ નું મૂલ્ય કેટલું હશે?View Solution
- 4$998\,\Omega$ અવરોધનું એક વોલ્ટમીટર $2$ વોલ્ટના એક વિધુત કોષ સાથે જોડાયેલું છે. તેનો આંતરિક અરોધ $2\,\Omega$ છે. $emf$ ના માપનમાં ક્ષતિ........હશે.View Solution
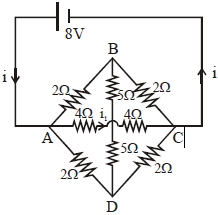
- 5પરિપથમાં $A$ થી $C$ તરફ વહેતા પ્રવાહ $i_{1}$ ........ $A$View Solution
- 6જ્યારે $4\,A$ જેટલો પ્રવાહ પસાર થાય છે ત્યારે એેક અવરોધમાં $10\,s$ માં $H$ મૂલ્યની ઉષ્મીય ઊર્જા ઉત્પન્ન થાય છે.જો પ્રવાહ વધારીને $16\,A$ કરવામાં આવે તો અવરોધમાં $10\,s$માં ઉત્પન્ન થતી ઉષ્મીય ઊર્જા $.......\,H$ થશે.View Solution
- 7View Solutionતારનો વ્યાસ ખેંચીને અડધો કરતાં અવરોધ કેટલા ગણો થાય?
- 8$r$ ત્રિજયાવાળા $i$ પ્રવાહધારિત તારમાં ઇલેકટ્રોનનો ડ્રિફટ વેગ $v$ છે, તો સમાન દ્રવ્ય અને અડધી ત્રિજયા ધરાવતા તારમાં $2v$ ડ્રિફટવેગ જોઇતો હોય,તો કેટલો પ્રવાહ પસાર કરવો પડે?View Solution
- 9બે વિધુત બલ્બ જેમના અવરોધોનો ગુણોત્તર $1 : 2$ છે. તેમને સમાંતરમાં જોડી અચળ વોલ્ટેજ આપેલ છે તો તેમાં વ્યય થતા પાવરનો ગુણોત્તર .. હશે.View Solution
- 10એક વ્હીસ્ટન બ્રિજની ચાર ભુજાઓ $P,Q,R$ અને $S$ ના અવરોધો અનુક્રમે $10\,Ω,\,30\,Ω,\,30\,Ω $ અને $90\,Ω$ છે.કોષનો $emf $ અને આંતરિક અવરોધ અનુક્રમે $7\,V$ અને $5\,Ω $ છે.જો ગેલ્વેનોમિટરનો અવરોધ $50\,Ω $ હોય,તો કોષમાંથી નીકળતો પ્રવાહ ................ $A$ હશે.View Solution
