આકૃતિમાં દર્શાવ્યા પ્રમાણે એક રિંગને $S$ બિંદુથી જડિત કરેલ છે.જયારે તેને સંતુલનથી સ્થાનતરિત કરવામાં આવે ત્યારે તે $1\,second$ ના આવર્તકાળથી ડોળાનો કરે છે.તો રીંગની ત્રિજ્યા $m$ માં કેટલી હશે?
($g = \pi ^2$ )
AIEEE 2012, Diffcult
Download our app for free and get started
a
We know that the time period of a physical pendulum is given by \(T=2 \pi \sqrt{\frac{I_{\text {support }}}{m g l_{\text {cm }}}}\)
We know that the time period of a physical pendulum is given by \(T=2 \pi \sqrt{\frac{I_{\text {support }}}{m g l_{\text {cm }}}}\)
\(I_{\text {support }}=m R^{2}+m R^{2}=2 m R^{2}\)
\(T=2 \pi \sqrt{\frac{\left(2 m R^{2}\right)}{m g R}} =2 \pi \sqrt{\frac{2 R}{g}}\)
\(\Rightarrow R=\frac{T^{2} g}{8 \pi^{2}}\)
A seconds pendulum is a pendulum whose period is precisely \(two\, seconds; one \,second\) for a swing in one direction and \(one\, second\) for the return swing. Ie. \(T=2 \varepsilon,\) so we have
\(R=\frac{2^{2} \times \pi^{2}}{8 \pi^{2}}=0.5 \mathrm{m}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કણ $X-$ અક્ષ પર સરળ આવર્તગતિ કરે છે, તો તેના પર લાગતું બળ શેના વડે આપી શકાય?View Solution
જ્યાં $A$ અને $K$ ધન અચળાંકો છે.
- 2સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $ x = 12\sin \omega t - 16{\sin ^3}\omega t $ હોય,તો મહત્તમ પ્રવેગ કેટલો થાય?View Solution
- 3કંપવિસ્તાર $2\ m$ અને આવર્તકાળ $2\ seconds$ ધરાવતી સરળ આવર્તગતિનો મહત્તમ વેગ કેટલો થાય?View Solution
- 4રેખીય સરળ આવર્ત ગતિમાંView Solution
$(A)$ પુન:સ્થાપક બળ સ્થાનાંતરના સમપ્રમાણમાં હોય છે.
$(B)$ પ્રવેગ અને સ્થાનાંતર વિરૂદ્ધ દિશામાં હોય છે.
$(C)$ મધ્ય સ્થાને વેગ મહત્તમ હોય છે.
$(D)$ અંત્ય બિંદુએ પ્રવેગ ન્યૂનત્તમ હોય છે.
નીચે આપેલા વિધાનોમાંથી સાચો ઉત્તર પસંદ કરો.
- 5સરળ આવર્ત ગતિ કરતાં સાદા લોલકનો આવર્તકાળ $T$ છે. જો લોલકની લંબાઇમાં $21\%$ નો વધારો કરવામાં આવે તો વધારેલી લંબાઈના લોલકનાં આવર્તકાળમાં કેટલો વધારો ($\%$) થાય?View Solution
- 6બે સરળ આવર્ત ગતિના સમીકરણView Solution
$x_{1}=5 \sin \left(2 \pi t+\frac{\pi}{4}\right), x_{2}=5 \sqrt{2}(\sin 2\pi t+\cos 2 \pi t).$
તો $x_{1}$ અને $x_{2}$ના કંપવિસ્તારનો ગુણોતર .....
- 7એક કણ $0.06 \mathrm{~m}$ કંપવિસ્તાર અને $3.14$ $s$ના આવર્તકાળ સાથે સરળ આવર્ત ગાત (સ.આ.ગ.) કરે છે. કણનો મહતમ વેગ. . . . . $\mathrm{cm} / \mathrm{s}$ હશે.View Solution
- 8View Solutionસરળ આવર્ત ગતિ કરતાં કણની કુલ ઉર્જા કોના સમપ્રમાણમાં હોય?
- 9View Solutionસરળ આવર્ત ગતિમાં ગતિપથમા મઘ્યમાન સ્થાને...
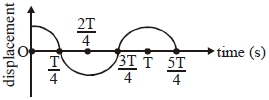
- 10સરળ આવર્ત ગતિ કરતાં કણ માટે સ્થાનાંતર વિરુદ્ધ સમયનો આલેખ આપેલ છે. તો તેના માટે નીચે પૈકી કેટલા વિધાનો સત્ય થશે?View Solution
$(A)$ $t=\frac{3 T}{4}$ સમયે બળ શૂન્ય થાય.
$(B)$ $t=T$ સમયે પ્રવેગ મહત્તમ થાય.
$(C)$ $t =\frac{ T }{4}$ સમયે વેગ મહત્તમ થાય.
$(D)$ $t=\frac{T}{2}$ સમયે ગતિઉર્જા અને સ્થિતિઉર્જા સમાન થાય.
