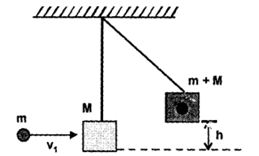
આકૃતિમાં દર્શાવ્યા પ્રમાણે મુક્ત કરેલા $M $ દળના એક લાકડાનો ટુકડા $ M$ દળની એક ગોળી $v_1$ વેગ સાથે અથડાય છે અને તેને ચોંટી જાય છે. જો ટુકડામાં $h $ ઉંચાઈ જેટલો વધારો થતો હોય તો ગોળીનો પ્રારંભિક વેગ કેટલો હશે ?

Medium
a
વેગમાં સરક્ષણ ના નિયમ પરથી, \(\,(m\,\, + \;\,M)\,\,v'\,\, = \,\,m{v_1}\)
વેગમાં સરક્ષણ ના નિયમ પરથી, \(\,(m\,\, + \;\,M)\,\,v'\,\, = \,\,m{v_1}\)
\(v'\,\, = \,\,\frac{{m{v_1}}}{{m\,\, + \,M}}\,\,\,.........\left( i \right)\)
હવે ઉર્જા સરક્ષણ ના નિયમ પરથી\(,\,\frac{1}{2}\,\,\left( {m\,\, + \;\,M} \right)\,\,{v^2}\,\, = \,\,\left( {m\,\, + \;\,M} \right)\,gh\)
\(\therefore \,\,v'\,\, = \,\sqrt {2gh} \,\,\,......\left( {ii} \right)\)
સમીકરણ(1) અને સમીકરણ(2) પરથી \(,{v_1}\,\, = \,\,\frac{{M\,\, + \;\,m}}{m}\,\,\sqrt {2gh} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$40kg$ ના પદાર્થનો વેગ $4m/s$ છે.અને $60kg$ના પદાર્થનો વેગ $2m/s$ છે.બંને વચ્ચે અસ્થિતિસ્થાપક સંધાત થાય,તો ગતિઊર્જામાં થતો ઘટાડો.....$J$View Solution
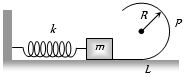
- 2સ્પ્રિંગને બ્લોક દ્વારા કેટલી દબાવીને મૂકવાથી $P$ બિંદુ આગળ કેન્દ્રગામી બળ $mg$ મળે?View Solution
- 3$100 gm$ દળનો એક પદાર્થ $r $ ત્રિજ્યા વક્ર પથ પર અચળ ઝડપથી ગતિ કરે છે. એક સંપૂર્ણ પરિભ્રમણ દરમિયાન થતું કાર્ય કેટલું હશે ?View Solution
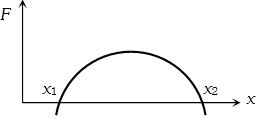
- 4$x$ -અક્ષની સાપેક્ષ પર ગતિ કરી રહેલાં એક પદાર્થ પર લાગતાં બળએ સ્થિતિ $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. પદાર્થ ક્યારે સ્થિર સંતુલિત સ્થિતિમાં હશે?View Solution
- 5એક પ્રક્ષિપ્ત પદાર્થની તેની મહત્તમ ઉંચાઈએ સ્થિતિ - ઊર્જા તેની શરૂઆતની ગતિઊર્જાની $3/4 $ ગણી થાય છે, તો પદાર્થનો પ્રક્ષિપ્તકોણ ...... $^o$ છે.View Solution
- 6એક કણ કે જે ફરજિયાત પણ $x-$ અક્ષ પર ગતિ કરે છે. તેના પર એ જ દિશામાં એક બળ લગાવવામાં આવે છે કે જે ઉગમબિંદુથી કણના અંતર $x$ સાથે $F(x) = -kx + ax^3$ અનુસાર બદલાય છે. જ્યા $k$ અને a ઘન અચળાંક છે. $x \ge 0$માટે પદાર્થની સ્થિતિ ઊર્જા $U (x)$ નો આલેખ કેવો હશે ?View Solution
- 7બે સમાન સ્પિંગ્રો $P$ અને $Q$ ના બળ અચળાંક અનુક્રમે $K_P $ અને $K_Q$ એવા છે, કે જયાં $K_P > K_Q$ છે. પ્રથમ વખત (કિસ્સો $a$) બંને સમાન લંબાઈથી ખેંચાય છે અને બીજી વખત (કિસ્સો $b$) સમાન બળ સાથે. સ્પ્રિંગ દ્વારા થતા કાર્ય અનુક્રમે $W_P$ અને $W_Q$ હોય, તો બંને કિસ્સા $(a)$ અને $(b)$ માં તેમની વચ્ચેનો સંબંધ અનુક્રમે શું થાય?View Solution
- 8વિધાન $-1$ અને વિધાન $-2$ આવેલા છે. જો $S_1$ અને $S_2$ બે સ્પ્રિંગના બળ અચળાંકો અનુક્રમે $k_1$ અને $k_2$ છે જેમને સમાન બળથી ખેંચેલી છે. એવું જાણવા મળ્યું કે $S_2$ સ્પ્રિંગ કરતા $S_1$ સ્પ્રિંગ પર થતું કાર્ય વધુ હોય છે.View Solution
વિધાન $1$ : જો સમાન મૂલ્યથી ખેંચવામાં આવે તો $S_1$ પર થતું કાર્ય જે $S_2$ પર થતા કાર્ય કરતા વધારે છે. વિધાન $2 : k_1 < k_2$
- 9View Solutionકણોના એેક તંત્ર અંદરની અંદર લાગતા આંતરિક બળો કોને બદલી શકે
- 10$m $ દળનો ગોળો $ v$ વેગથી બીજા સમાન દળના સ્થિર ગોળા સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંધાત અનુભવે છે,અથડામણ પછી પ્રથમ $m $ દળના ગોળાનો વેગ કેટલો થાય?View Solution
