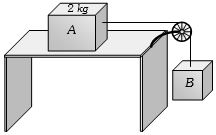
આકૃતિમાં દર્શાવ્યા પ્રમાણે ટેબલ પર $2\;kg$ નો બ્લોક $A$ રહેલ છે, તેમની વચ્ચેનો સ્થિત ઘર્ષણાક $0.2$ છે. બ્લોક $B$ નું મહત્તમ દળ ($kg$ માં) કેટલું હોવું જોઈએ કે જેથી બંને બ્લોક ખસે નહીં. દોરી અને ગરગડીને ઘર્ષણરહિત અને દળવિહીન ધારો. $(g = 10\,m/{s^2})$
AIPMT 2004, Medium
Download our app for free and get started
d
(d) \({\mu _s} = \frac{{{m_B}}}{{{m_A}}}\) \(⇒\) \(0.2 = \frac{{{m_B}}}{2}\) \(⇒\) \({m_B} = 0.4\;kg\)
(d) \({\mu _s} = \frac{{{m_B}}}{{{m_A}}}\) \(⇒\) \(0.2 = \frac{{{m_B}}}{2}\) \(⇒\) \({m_B} = 0.4\;kg\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20\,kg$ નો બ્લોક ઘર્ષણવાળી સપાટી પર સ્થિર પડેલ છે.તેને ગતિમાં લાવવા $75\, N $ નું સમક્ષિતિજ બળ જરૂર પડે છે.તે ગતિમાં આવ્યા પછી $60\, N$ નું બળ અચળ ઝડપ રાખવા માટે જરૂર પડે છે.તો સ્થિત ઘર્ષણાંક કેટલો થાય?View Solution
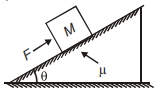
- 2એક બ્લોક દળ = $M \,kg $ ને એક ખરબચડી ઢોળાવવાળી સમતલ પર મુકવામાં આવે છે. એક બળ $F$ ને ઢાળની સમાંતર એવી રીતે લગાડવામાં આવે છે (આકૃતિમાં દર્શાવ્યા મુજબ) જેથી બ્લોક ઉર્ધ્વ દિશામાં તરત જ ગતિ કરે છે. તો $F$ નું મૂલ્ય કેટલું છેView Solution
- 3એક બ્લોક સમક્ષિતિજ સાથે $\alpha$ ખૂણો બનાવતા સમતલ પર સ્થિર પડેલો છે. જેવો $\alpha$ ખૂણો વધારવામાં આવે જ્યારે તેનો ખૂણો $\theta$ થાય ત્યારે બ્લોક સરકવાનું શરૂ કરે છે. બ્લોક અને ઢળતા સમતલ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
- 4$W$ વજનવાળો બ્લોક સમક્ષિતિજ સપાટી પર સ્થિત ઘર્ષણાંક $\mu$ થી સ્થિર છે. બ્લોક પર ન્યુનત્તમ મૂલ્યનું બળ લગાવીને તેને ગતિ કરાવવામાં આવે છે. સમક્ષિતિજથી એવો ખૂણો $\theta $ કે જ્યાથી બળ લગાવવામાં આવે અને બળનું મૂલ્ય અનુક્રમે શું થાય?View Solution
- 5$200\,kg$ નું વજન ધરાવતું એક વાહન વક્રાકાર સમતલ ધરાવતા રસ્તા પર કે જેની ત્રિજ્યા $70\,m$ છે તેના પર $0.2\,rad / s$ ના કોણીય વેગ સાથે ગતિ કરે છે. વાહન પર લાગતું કેન્દ્રગામી બળ .......... $N$ છે.View Solution
- 6$10 \,kg$ દળ ધરાવતું એક ચોસલું સપાટી ઉપર $9.8 \,ms ^{-1}$ ના પ્રારંભિક વેગથી સરકવાનું શરૂ કરે છે. સપાટી અને ચોસલા નો ઘર્ષણક $0.5$ છે. વિરામસ્થિતિમાં આવતા પહેલા ચોસલાએ કાપેલું અંતર .........$m$ હશે.View Solution
[ $g =9.8\, ms ^{-2}$ લો ]
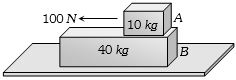
- 7એક $40 \,kg$ નાં સ્લેબ ઘર્ષણ રહિત સપાટી પર સ્થિર પડેલો છે. એક $10 \,kg$ નો બ્લોક સ્લેબ પર સ્થિર પડયો છે. બ્લોક અને સ્લેબ વચ્ચે સ્થિત ઘર્ષણાંક $0.6$ અને ગતિક ઘર્ષણાંક $0.4 $ છે. $10 \,kg$ બ્લોક પર $100 \,N$ નો સમક્ષિતિજ બળ લગાડવામાં આવે છે. જો $g=10 \,m / s ^2$ છે, તો સ્લેબનો પરિણામી પ્રવેગ ................ $m / s ^2$ હશેView Solution
- 8$m$ દળ ધરાવતા ટુકડાને $y = \frac{{{x^3}}}{6}$ જેટલો ઊભા આડછેદ ધરાવતી સપાટી પર મૂકવામાં આવે છે.જો ઘર્ષણાંક $ 0.5$ હોય,તો સરકયા સિવાય ટુકડાને જમીનથી ઉપર કેટલી મહત્તમ ઊંચાઇએ મૂકી શકાય.View Solution
- 9$800 \mathrm{~kg}$ ની એક કાર $300 \mathrm{~m}$ ની ત્રિજ્યાં અને $30^{\circ}$ ના કોણવાળા ઢોળાવ વાળા રોડ ઉપર વળાંક લે છે. જો સ્થિતિ ઘર્ષણાંક $0.2$ હોય તો સુરક્ષિત રીતે ગાડી આ વળાંક લઈ શકે તે માટે મહત્તમ ઝડપ . . . . .હશે. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73\right)$ લો.View Solution
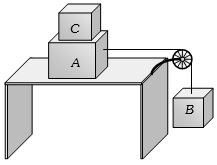
- 10$A$ અને $B$ ના દળ $10\,kg$ અને $5\,kg$ છે,$A$ અને ટેબલ વચ્ચેનો ઘર્ષણાક $0.2$ છે.$C$ નું લઘુત્તમ દળ ....... $kg$ હોવું જોઈએ કે જેથી $A$ ખસે નહિ.View Solution
