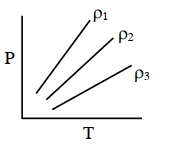
આકૃતિમાં ત્રણ જુદી-જુદી ધનતા $\rho_1, \rho_2, \rho_3$ (ત્રણ જુદા-જુદા કિસ્સામાં) ધરાતવા આદર્શ વાયુ માટે $P-T$ ડાયાગ્રામ દર્રાવેલ છે. નીચેનામાંથી ક્યું સાચુ છે ?

JEE MAIN 2024, Diffcult
b
For ideal gas
For ideal gas
\(P V=n R T\)
\(P V=\frac{m}{M} R T\)
\(P=\left(\frac{M}{V}\right) \frac{R T}{M}\)
\(P=\frac{\rho R T}{M}\)
(Where \(\mathrm{m}\) is mass of gas and \(\mathrm{M}\) is molecular mass of gas)
for same temperature \(\mathrm{P}_1>\mathrm{P}_2>\mathrm{P}_3\)
So \(\rho_1>\rho_2>\rho_3\)
So correct answer is \((2)\)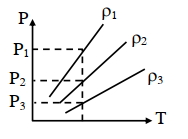
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1....... $^oC$ તાપમાને હાઈડ્રોજન પરમાણુની સરેરાશ ઝડપ એ $31°C$ એ પહેલા ઓક્સિજન પરમાણુની સરેરાશ ઝડપ કેટલી થશે?View Solution
- 2$CO_2 (O - C - O)$ એ ત્રિઆણ્વિય વાયુ છે. વાયુના $1\,gm$ ની સરેરાશ ગતિ ઊર્જા ......છે. $N$એ એવોગેડ્રો અંક, $k $- બોલ્ટઝમેન અચળાંક અને $CO_2$ નો અણુભાર $=44$View Solution
- 3$10$ વાતાવરણના દબાણે અને $57^{\circ} C$ તાપમાને $28$ ગ્રામ નાઈટ્રોજન વાયુ એક પાત્રમાં ભરવામાં આવ્યો છે. છીદ્રમાંથી અનુસ્રાવ થતાં $N _2$ નું દબાણ $5$ વાતાવરણ અને તાપમાન $27^{\circ} C$ થઈ જાય તો .............. $g$ $N _2$ વાયુ બહાર નીકળી ગયો હશે.View Solution
- 4$300 K$ તાપમાને રહેલ પાત્રમાં એક મોલ ઓક્સિજન અને બે મોલ નાઇટ્રોજન વાયુ ભરેલ છે.${O_2}$ની સરેરાશ ચાકગતિઉર્જા અને ${N_2}$ ની સરેરાશ ચાકગતિઉર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 5એક ત્રિપરમાણ્વિક વાયુ છે. તેના અણુંનો આકાર ત્રિકોણાકાર અને તેમના પરમાણુ ત્રિકોણના શિરોબિંદુ પર દળરહિત સળીયાથી જોડાયેલા છે. તો $T$ તાપમાને વાયુના એક મોલની આંતરિક ઊર્જા $........RT$ થશે.View Solution
- 6$\upsilon _1, \upsilon _2, \upsilon _3 $…..…$n $ ઝડપ ધરાવતાં વાયુમાં $n$ અણુઓની $rms$ ઝડપ =........View Solution
- 7એક મોલ એક પરમાણ્વિય વાયુને ત્રણ મોલ દ્વિ- પરમાણ્વીય વાયુ સાથે નિશ્વિત કરવામાં આવે છે. આ મિશ્રણની અચળ કદે મોલર વિશિષ્ટ ઉષ્મા $\frac{\alpha^2}{4} R\,J / mol K$ છે $\alpha$ નું મૂલ્ય થશે.View Solution
- 8વાયુ માટેનું સમીકરણ નીચે મુજબ આપવામાં આવે છેView Solution
$\left( {P + \frac{{a{T^2}}}{V}} \right)\,{V^c} = (RT + b)$, જ્યાં $a, b, c$ અને $R$ અચળાંક છે.
તે સમતાપી રીતે $P = A{V^m} - B{V^n}$ પર આધાર રાખે જ્યાં $A$ અને $B$ માત્ર તાપમાન પર આધાર રાખતા હોય તો ...
- 9$ 0^\circ C $ તાપમાને બેરોમીટરનું દબાણ $760\, mm$ છે.તો $ 100^\circ C $ તાપમાને બેરોમીટરનું દબાણ કેટલું થાય?View Solution
- 10$1$ મોલ આદર્શ એક પરમાણ્વીય વાયુનું અચળ $P$ તાપમાન $20°C$ થી $30°$ કરવા $40\, Cal$ ની જરૂર પડે છે. તો આજ તાપમાનમાં વધારો અચળ કદે કરતાં ....... $cal$ ઊર્જાની જરૂર પડે ?View Solution
