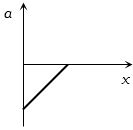
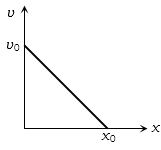
આપેલ આલેખ વેગ વિરુદ્ધ સ્થાનાંતર નો વક્ર દર્શાવે છે.તો નીચેનામાથી કયો આલેખ પ્રવેગ વિરુદ્ધ સ્થાનાંતર ના વક્ર માટે સાચો છે?

IIT 2005, Diffcult
a
(a) Given line have positive intercept but negative slope. So its equation can be written as
(a) Given line have positive intercept but negative slope. So its equation can be written as
\(v = - mx + {v_0}\)…..(i) [where \(m = \tan \theta = \frac{{{v_0}}}{{{x_0}}}\)]
By differentiating with respect to time we get \(\frac{{dv}}{{dt}} = - m\frac{{dx}}{{dt}} = - mv\)
Now substituting the value of \(v\) from eq. (i) we get \(\frac{{dv}}{{dt}} = - m[ - mx + {v_0}] = {m^2}x - m{v_0}\)
\(\therefore a = {m^2}x - m{v_0}\)
i.e. the graph between \(a\) and \(x\) should have positive slope but negative intercept on \(a-\)axis. So graph \((a) \) is correct.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ચોક્કસ ઊંચાઈ $h$ ($h$ ખૂબ મોટી છે) થી એક પદાર્થને મુક્ત પતન કરવામાં આવે છે અને બીજા પદાર્થને $5 \,m / s$ ના વેગ સાથે નીચેની તરફ ફેકવામાં આવે છે. $3 \,s$ પછી બે પદાર્થની ઊંચાઈમાં ........... $m$ તફાવત હશે ?View Solution
- 2પ્રારંભિક સ્થિર અવસ્થામાંથી કણ $\frac{4}{3}\ ms^{-2}$ ના પ્રવેગથી ગતિ કરે છે. કણે ત્રીજી સેકન્ડમાં કાપેલું અંતર કેટલું હશે?View Solution
- 3$h$ ઊંચાઇ અને $l $ લંબાઇ ધરાવતા $\theta $ ખૂણાવાળા ઢાળ પરથી પદાર્થને ઉપરથી નીચે આવતા કેટલો સમય લાગે?View Solution
- 4એક ગ્રહ પર બોલને $100\; m$ ઊંચાઈના ટાવર પરથી મુક્ત કરવામાં આવે છે. જમીન પર પહોચતા પહેલા છેલ્લી $\frac{1}{2}\;s $ માં તે $19\; m$ અંતર કાપે છે. ગ્રહની સપાટી નજીક ગુરુત્વ પ્રવેગનું મૂલ્ય (${ms}^{-2}$ માં) કેટલું હશે?View Solution
- 5$40 \ km/h$ ની ઝડપથી ગતિ કરતાં એક વાહનને બ્રેક મારતા તે $40 m$ અંતર કાપીને સ્થિર થાય છે. જો તે જ વાહન $80 \ km/h$ ની ઝડપથી ગતિ કરતું હોય, તો તેને રોકવા માટેનું ન્યુનત્તમ અંતર $($સ્ટોપિંગ અંતર$) ..........(m) ($મીટરમાં$)$ કેટલું હશે? $($વાહન સરકતું નથી તેવું ધારો$)$View Solution
- 6એક કણનો વેગ $(4{t^3} - 2t)$ સૂત્ર મુજબ છે,કણ ઉદ્ગમ બિંદુથી $2m$ અંતરે હોય ત્યારે તેનો પ્રવેગ કેટલા..........$m/{s^2}$ હશે?View Solution
- 7${m_1}$ અને ${m_2}$ દળના બોલને સમાન ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે તો તેને જમીન પર આવતા લાગતો સમય ${t_1}$ અને ${t_2}$ હોય તોView Solution
- 8પદાર્થને એક ઢાળ પર ઉપરથી નીચે પહોચતા $4\, sec$ લાગે તો તેના ચૌથા ભાગનુ અંતર કાપતા કેટલા.........$s$ નો સમય લાગે?View Solution
- 9જો $t =\sqrt{ x }+4$ છે, તો $\left(\frac{ dx }{ dt }\right)_{ t =4}$ નું મૂલ્ય.View Solution
- 10એક બોલને $h$ ઊંચાઈએથી છોડવામાં આવે છે. જો $t_1$ અને $t_2$ અનુક્રમે અંતરના પ્રથમ અર્ધભાગ અને પછીના અર્ધભાગ માટેના સમય છે. તો $t_1$ અને $t_2$ વચ્ચેનો સાચો સંબંધ પસંદ કરો.View Solution