Download App
આપેલ લોજીક પરિપથ માટે સત્યાર્થી સારણી (ટ્રુથ ટેબલ)$.......$ છે.
  • A
    $A$ $B$ $C$
    $0$ $1$ $0$
    $0$ $1$ $0$
    $1$ $0$ $0$
    $1$ $1$ $1$

     

  • B
    $A$ $B$ $C$
    $0$ $0$ $1$
    $0$ $1$ $0$
    $1$ $0$ $1$
    $1$ $1$ $0$

     

  • C
    $A$ $B$ $C$
    $0$ $0$ $0$
    $0$ $1$ $0$
    $1$ $0$ $0$
    $1$ $1$ $1$

     

  • D
    $A$ $B$ $C$
    $0$ $0$ $0$
    $0$ $1$ $1$
    $1$ $0$ $1$
    $1$ $1$ $0$
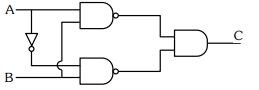
NEET 2022, Medium
Download our app for free and get startedPlay store
b
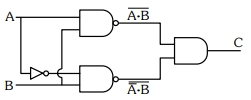
\(C=\overline{A \cdot B} \cdot \bar{A} \cdot B\)

using De-Morgan Theorem

\(C=\overline{A \cdot B+\bar{A} \cdot B}\)

\(C=\overline{B(A+\bar{A})}=\bar{B}\)

Therefore

\(A\) \(B\) \(C\)
\(0\) \(0\) \(1\)
\(0\) \(1\) \(0\)
\(1\) \(0\) \(1\)
\(1\) \(1\) \(0\)

 

art

Download our app
and get started for free

Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Download App

Similar Questions

  • 1
    નેગેટિવ લોજીક પદ્વિતમાં આપેલ તરંગ માટે નીચેનામાથી શું સાચું થાય?
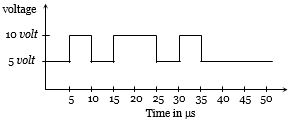
    View Solution
  • 2
    નીચેનામાંથી કયો ડાયોડ ફોરવર્ડ બાયસમાં છે?
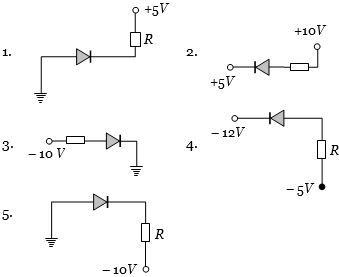
    View Solution
  • 3
    ટ્રાન્ઝીસ્ટરમાં કલેક્ટર વિદ્યુતપ્રવાહ હંમેશા એમીટર વિદ્યુતપ્રવાહ કરતાં ઓછા હોય છે. કારણ કે,
    View Solution
  • 4
    શુદ્ધ સિલિકોનના સેમ્પલમાં $10^{13} atom/cm^3 $ જેટલામાં ફોસ્ફરસ મિશ્ર કરવામાં આવે છે. જો બધા ડોનર અણુઓ સક્રિય હોય અને ઈલેક્ટ્રોનની મોબિલીટી $1200 cm^2/ volt$  $sec$ હોય તો $20° C $ એ અવરોધકતા કેટલા ......$\Omega$ $cm$ હશે?
    View Solution
  • 5
    જેમ તાપમાન વધે તેમ વિદ્યુતકિય અવરોધ ......
    View Solution
  • 6
    સોલાર સેલનો કાર્યરત વિસ્તાર ...... હોય છે જેથી મળતો પાવર ......
    View Solution
  • 7
    કોમન એમિટર ટ્રાન્ઝીસ્ટર માટે આઉટપુટ અવરોધ $500\,k\Omega $, પ્રવાહ ગેઈન $\alpha = 0.98$ અને પાવર ગેઈન $6.0625 \times 10^6$ હોય તો ઈનપુટ અવરોધ ........ $\Omega $
    View Solution
  • 8
    $P$ પ્રકારના અર્ધવાહકમાં એક્સેપ્ટરનું પ્રમાણ $57\;me V$  થી ઉપર વેલેન્સ બેન્ડ છે. તો મહત્તમ પ્રકારની તરંગ લંબાઈ કેટલી હશે કે જેથી હોલનું નિર્માણ થઈ શકે?
    View Solution
  • 9
    નીચે બે વિધાનો આપેલા છે : તેમાંના એકને કથન $A$ અને બીજાને કારણ $R$ થી દર્શાવવામાં આવેલ છે.

    કથન $A$ : $n-p-n$ ટ્રાન્ઝિસ્ટર, $p-n-p$ ટ્રાન્ઝિસ્ટર કરતા વધારે પ્રવાહ પસાર થવા દે છે.

    કારણ $R$ : ઈલેકટ્રોનની વિદ્યુત વાહક તરીકેની મોબીલીટી વધારે હોય છે.

    ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પો પૈકી સૌથી યોગ્ય ઉત્તર પસંદ કરો.

    View Solution
  • 10
    $N$- પ્રકારનો અર્ધવાહકને ગરમ કરવામાં આવે, ત્યારે .....
    View Solution