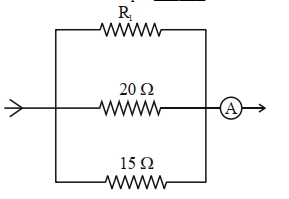
આપેલ પરિપથમાં, $20 \Omega$ અવરોધમાં વહેતો પ્રવાહ $0.3$ $A$ હોય , જ્યારે એમિટર $0.9$ $A$નું અવલોકન નોંધે છે. $R_1$ નું મૂલ્ય___________$\quad \Omega છ$.

JEE MAIN 2024, Diffcult
d
Given, \(i_1=0.3 \mathrm{~A}, \mathrm{i}_1+\mathrm{i}_2+\mathrm{i}_3=0.9 \mathrm{~A}\)
Given, \(i_1=0.3 \mathrm{~A}, \mathrm{i}_1+\mathrm{i}_2+\mathrm{i}_3=0.9 \mathrm{~A}\)
So, \(\mathrm{V}_{\mathrm{AB}}=\mathrm{i}_1 \times 20 \Omega=20 \times 0.3 \mathrm{~V}=6 \mathrm{~V}\)
\( \mathrm{i}_2=\frac{6 \mathrm{~V}}{15 \Omega}=\frac{2}{5} \mathrm{~A} \)
\( \mathrm{i}_1+\mathrm{i}_2+\mathrm{i}_3=\frac{9}{10} \mathrm{~A} \)
\( \frac{3}{10}+\frac{2}{5}+\mathrm{i}_3=\frac{9}{10} \)
\( \frac{7}{10}+\mathrm{i}_3=\frac{9}{10} \)
\( \mathrm{i}_3=0.2 \mathrm{~A} \)
\( \text { So, } \mathrm{i}_3 \times \mathrm{R}_1=6 \mathrm{~V} \)
\( (0.2) \mathrm{R}_1=6 \)
\( \mathrm{R}_1=\frac{6}{0.2}=30 \Omega\)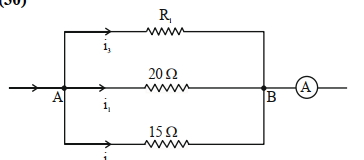
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
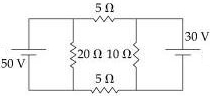
- 1આપેલ પરિપથમાં રહેલ $50\, V$ અને $30\, V$ ની બેટરીમાંથી અનુક્રમે કેટલો પ્રવાહ($A$ માં) પસાર થાય?View Solution
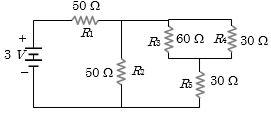
- 2આપેલ પરિપથમાં અવરોધ $R_4$ નો વોલ્ટેજ કેટલા ............... $V$ થાય?View Solution
- 3$R$ અવરોધ અને $L$ લંબાઈના તારને $5$ એકસરખા ભાગમાં કાપવામાં આવે છે. તે પ્રત્યેક ભાગને એકબીજા સાથે સમાંતર જોડવામાં આવે તો પરિણામી અવરોધ______થશે.View Solution
- 4$800\,^oC$ તાપમાને હીટરનો પાવર $500\,W$ છે. તો $200\,^oC$ તાપમાને પાવર કેટલા .............. $W$ હશે ? તેનો $\alpha$ = $4 \times 10^{-4}/\,^oC$.View Solution
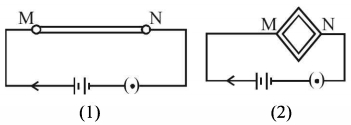
- 5આકૃતિ $(1)$ માં બતાવ્યા મુજબ બિંદુ $M$ એ $N$ વચ્ચેના વાયરને બેટરી સાથે જોડેલ છે. આકૃતિ $(2)$ મુજબ તે વાયરને ચોરસના રૂપમાં વાળીને બે બિંદુઓ વચ્ચેથી બેટરી સાથે જોડેલ છે. નીચેનામાથી કઈ રાશિમાં વધારો થશે.View Solution
- 6$V_0$ વોલ્ટેજ એક વિધુત બલ્બ (ગોળો), $P_0$ પાવર આપે છે. જો વોલ્ટેજ $V$ હોય તો તે …$P$ પાવર આપે છે.View Solution
- 7મીટર બ્રીજ પ્રયોગમાં જ્યારે $X$ અવરોધ બીજા $Y$ અવરોધની વિરૂદ્ધમાં હોય ત્યારે તારના એક છેડાથી $20\, cm$ અંતેર શૂન્ય બિંદુ મળે છે. જો $X < Y$ હોય તો સમાન છેડાથી શૂન્ય બિંદુનું નવું સ્થાન ક્યાં હશે ? તે $Y$ ની વિરૂદ્ધમાં $4X$ અવરોધનું સંતુલન ...................... $cm$ નક્કી કરે છે ?View Solution
- 8$10 $ કોષ ધરાવતી $ 5$ હારને અવરોઘ $20 \,\Omega $ સાથે સમાંતરમાં જોડવામાં આવે છે,જો કોષનો $ emf \,1.5\, volt $ અને આંતરિક અવરોઘ $ 1\, \Omega $ હોય,તો બાહ્ય અવરોધમાં પસાર થતો પ્રવાહ $i$ હોય તો પ્રવાહનું મૂલ્ય કેટલું થાય?View Solution
- 9બે એકસમાન પરિમાણ ધરાવતા ધાત્વીય તારોને શ્રેણીમાં જોડવામાં આવેલા છે. જે $\sigma_1$ અને $\sigma_2$ એ આ તારોની અનુક્રમે વાહકતા હોય, તો આ સંયોજનની અસરકારક વાહકતા $..........$ થશે.View Solution
- 10View Solutionજ્યારે એક ધાતુના તારના છેડાઓ વચ્ચે અચળ વોલ્ટેજ લાગુ પાડવામાં આવે તો આ તારમાં ઉત્પન્ન થતી ઉષ્મા બમણી હશે તો.....
