આયર્ન માંથી બે પ્લેટ $A$ અને $B$ બનાવેલ છે જેની ત્રિજ્યા અનુક્રમે $r$ અને $4r$ અને જાડાઈ અનુક્રમે $t$ અને $t/4$ છે. $A$ અને $B$ ની જડત્વની ચાકમાત્રા $I_A $ અને $I_B $ હોય તો તેમની વચ્ચેનો સંબંધ .
Medium
c
Moment Of Inertia \(=I=\frac{M R^{2}}{2}\)
Moment Of Inertia \(=I=\frac{M R^{2}}{2}\)
Mass \(=\) Density\(\times\)Volume
Let \(d\) be the density of both the iron plate
Using the above equations,
\(I_{A}=(d)\) \(\times\) \(\Pi r^{2} t \frac{r^{2}}{2}=\frac{\Pi d t r^{4}}{2}\)
\(I_{B}=d\) \(\times\) \(\Pi(4 r)^{2} \frac{t}{4} \frac{(4 r)^{2}}{2}=64 I_{A}\)
Moment Of Inertia \(=I=\frac{M R^{2}}{2}\)
Mass \(=\) Density\(\times\)Volume
Let \(d\) be the density of both the iron plate
Using the above equations,
\(I_{A}=(d)\) \(\times\) \(\Pi r^{2} t \frac{r^{2}}{2}=\frac{\Pi d t r^{4}}{2}\)
\(I_{B}=d\) \(\times\) \(\Pi(4 r)^{2} \frac{t}{4} \frac{(4 r)^{2}}{2}=64 I_{A}\)
Therefore, \(I_{A} < I_{B}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\ cm $ ત્રિજ્યા અને $5\ mm $ જાડાઈ ધરાવતી એક વર્તૂળાકાર તકતીની નિયમિત ઘનતા $8 \ g/cc$ છે. આ તકતીને લંબ અને તેના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને આ તકતીની જડત્વની માત્રા શોધો.View Solution
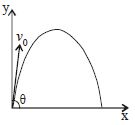
- 2એક નાના $m$ દળના કણને $x-$અક્ષ સાથે $\theta $ ખૂણે $V_0$ વેગથી $X-Y$ સમતલમાં ફેકતા તે આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. $t < \frac{{{v_0}\,\sin \,\theta }}{g}$ સમયે કણનું કોણીય વેગમાન કેટલું હશે?View Solution
- 3View Solutionવર્તૂળાકાર પ્લેટફોર્મની કિનારી પર માણસ ઉભેલો છે. પ્લેટફોર્મના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષ પર તે અચળ કોણીય ઝડપથી ભ્રમણ કરે છે. જો માણસ ત્રિજ્યા પર ચાલીને અક્ષ તરફ જતો હોય ત્યારે કોણીય વેગ ........ થશે.
- 4View Solutionજો એક બોમ્બ ને સમક્ષિતિજ સાથે થોડાક ખૂણે ફેકવામાં આવે છે અને બોમ્બ ફુટયા પછી તેના ટુકડા અલગ અલગ દિશામાં પડતાં હોય તો દ્રવ્યમાનકેન્દ્ર ....
- 5$200\ gm$ અને $500\ gm$ ના પદાર્થના વેગ $10\hat i m/s$ અને $3\hat i + 5\hat j m/s$ છે.તો દ્રવ્યમાન કેન્દ્ર નો વેગ કેટલો થાય?View Solution
- 6એક વર્તૂળાકાર તકતી $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. જો તકતી પર બાળક બેસે, તો શેનું સંરક્ષણ થશે ?View Solution
- 7View Solutionએક પાતળી વર્તુળાકાર વીટી સૌપ્રથમ એક ઢોળાવયુક્ત સપાટી ઉપરથી નીચે સરકે છે અને ત્યાર બાદ તેજ ઊંચાઈથી સમાન ભૂમિતિના એક ખરબચડા ઢોળાવ ઉપરથી નીચે ગબડે છે. બે ગતિઓમાં લેવાયેલ સમયનો ગુણોત્તર શું થાય?
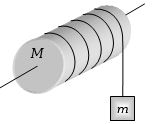
- 8$m=M$ દળનો પદાર્થ મુકત કરતાં,તે કેટલા પ્રવેગથી ગતિ કરશેView Solution
- 9$5\ kg$ દળ ધરાવતા સ્થિર પૈડા પર $30\ Nm $ જેટલું ટૉર્ક $15 $ સેકન્ડ માટે લગાડવામાં આવે છે. પૈડાની જડત્વની ચાકમાત્રા $2\ kg\ m^2$ છે. આ $10$ સેકન્ડમાં પૈડાએ કરેલું કોણીય સ્થાનાંતર ....... $\ rad$View Solution
- 10$2\,kg$ દળ અને $0.5\, m$ ત્રિજ્યા ધરાવતો ગોળો $1 \,ms ^{-1}$ ના વેગથી $30^{\circ}$ ખૂણાવાળા ઢાળ પર ઉપર તરફ ગતિ કરે છે. તો તેને બિંદુ $A$ પર પાછા આવતા કેટલો સમય ($sec$) લાગશે?View Solution