અચળ તાપમાન પર નીચે આપેલી પ્રથમ ક્રમ વાયુઅવસ્થા પ્રક્રિયાને ધ્યાનમાં લો.
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$23 \mathrm\ {sec}$ પછી જો વાયુઆનું કુલ દબાણ $200\ torr$ મળી આવેલ હોય અને ખુબજ લાંબા સમય બાદ $A$ નાં સંપૂર્ણ વિધટન પર $300\ torr$ મળી આવેલ હોય તો આપેલ પ્રક્રિયા નો વેગ અચળાંક ......... $\times 10^{-2} \mathrm{~s}^{-1}$ છે. [આપેલ : $\left.\log _{10}(2)=0.301\right]$
JEE MAIN 2024, Medium
Download our app for free and get started
a
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$\mathrm{P}_{23}=\mathrm{P}_0+2 \mathrm{x}=200$
$\mathrm{P}_{\infty}=3 \mathrm{P}_0=300$
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$\mathrm{P}_{23}=\mathrm{P}_0+2 \mathrm{x}=200$
$\mathrm{P}_{\infty}=3 \mathrm{P}_0=300$
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$\mathrm{P}_{23}=\mathrm{P}_0+2 \mathrm{x}=200$
$\mathrm{P}_{\infty}=3 \mathrm{P}_0=300$
$\mathrm{P}_0=100$
$\mathrm{~K}=\frac{1}{\mathrm{t}} \ln \frac{\mathrm{P}_{\infty}-\mathrm{P}_0}{\mathrm{P}_{\infty}-\mathrm{P}_{\mathrm{t}}}$
$\mathrm{K}=\frac{2.3}{23} \log \frac{300-100}{300-200}$
$=\frac{2.3 \times 0.301}{23}=0.0301=3.01 \times 10^{-2} \mathrm{sec}^{-1}$
$\mathrm{P}_0=100$
$\mathrm{~K}=\frac{1}{\mathrm{t}} \ln \frac{\mathrm{P}_{\infty}-\mathrm{P}_0}{\mathrm{P}_{\infty}-\mathrm{P}_{\mathrm{t}}}$
$\mathrm{K}=\frac{2.3}{23} \log \frac{300-100}{300-200}$
$=\frac{2.3 \times 0.301}{23}=0.0301=3.01 \times 10^{-2} \mathrm{sec}^{-1}$
$\mathrm{P}_0=100$
$\mathrm{~K}=\frac{1}{\mathrm{t}} \ln \frac{\mathrm{P}_{\infty}-\mathrm{P}_0}{\mathrm{P}_{\infty}-\mathrm{P}_{\mathrm{t}}}$
$\mathrm{K}=\frac{2.3}{23} \log \frac{300-100}{300-200}$
$=\frac{2.3 \times 0.301}{23}=0.0301=3.01 \times 10^{-2} \mathrm{sec}^{-1}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રથમ ક્રમની પ્રક્રિયાને $90\%$ પુરી પાડવા $10$ કલાક જેટલો સમય લાગે છે તો $99.9\%$ પ્રક્રિયા પૂર્ણ થવા કેટલો સમય લાગે?View Solution
- 2પ્રક્રિયા $X \rightleftharpoons Y$ માટે પુરોગામી અને પ્રતિગામી પ્રક્રિયાનો પૂર્વધાતાંક અવયવ સમાન છે. તો પ્રક્રિયાનો સંતુલન અચળાંક કેટલો થશે ?View Solution
- 3$aG + bH \rightarrow$ નિપજ પ્રક્રિયાને ધ્યાનમાં લેતાં જ્યારે $G$ અને $H$ બંને પ્રક્રિયકોની સાંદ્રતા બમણી હોય તો દર વધીને $8$ ગણું થાય છે. જો કે જ્યારે $G$ ની સાંદ્રતા બમણી થાય ત્યારે $H$ ની સાંદ્રતા નિયત રહે તો દર બમણો થશે. તો સમગ્ર પ્રક્રિયાનો ક્રમ શું થશે?View Solution
- 4$25^{\circ} C$ પર $3.33\, h$ અર્ધ-આયુષ્ય સાથે, સુક્રોઝ એસિડ દ્રાવણમાં ગ્લૂકોઝ અને ફ્રૂકટોઝમાં જળવિભાજન પામે છે જે પ્રથમ ક્રમ વેગ નિયમને અનુસરે છે. $9\, h$ પછી, સુક્રોઝનો અંશ $f$ બાકી રહે છે. તો $\log _{10}\left(\frac{1}{f}\right)$ નું મૂલ્ય ..... $\times 10^{-2}$ છે.View Solution
(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ) (ધારી લો : $\ln 10=2.303, \ln 2=0.693$)
- 5$2A + B \rightarrow $ નીપજ પ્રક્રિયામાં $B$ નું સાંદ્રણ બમણું કરવામાં આવે તો અર્ધ આયુષ્ય સમય બદલાતો નથી. પરંતુ જ્યારે ફક્ત $A$ ની સાંદ્રતા બમણી કરવામાં આવે તો વેગ બમણો થાય છે. તો આ પ્રક્રિયા માટે વેગ અચળાંકનો પરિમાણ (એકમ) જણાવો.View Solution
- 6એસ્ટરના જળવિભાજન માટે વેગઅચળાંક પર $pH$ ની અસર .......... દ્વારા આપવામાં આવે છે.View Solution
- 7ધુમ્મસના ઘટક પેરોક્સિ એસિટાઇલ નાઇટ્રેટ $(PAN)$ નુ વિઘટન પ્રથમ ક્રમની પ્રક્રિયા મુજબ પેરોક્સિ એસિટઇલ રેડિકલ અને $N{O_{2\left( g \right)}}$ માં થાય છે, જેનો અર્ધઆયુષ્ય સમય $32\,\min$ છે.View Solution
$\begin{matrix}
O\,\,\,\,\,\,\, \\
||\,\,\,\,\,\,\, \\
C{{H}_{3}}-C-OON{{O}_{2}} \\
\end{matrix}$ $\to$ $\begin{matrix}
\,\,\,\,\,\,\,\,\,\,\,O\,\,\,\,\,\,\,\, \\
\,\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\, \\
C{{H}_{3}}-C-O\overset{\centerdot }{\mathop{O}}\, \\
\end{matrix}$ $ + N{O_2}$જો હવાના નમૂનામાં $PAN$ ની શરૂઆતની સાંદ્રતા $5.0 \times 10^{14}\, molecules/L$ હોય તો $1.5\, hr$ પછી સાંદ્રતા કેટલી થશે ?
- 8$320\,^o C$ તાપમાને પ્રથમ ક્રમની પ્રક્યિાView Solution
$S{{O}_{2}}C{{l}_{2}}\to S{{O}_{2}}+C{{l}_{2}}$ નો વેગ અચળાંક $2.2 \times 10^{-5}\, s^{-1}$ છે. આ વાયુને $90\, min$ સુધી ગરમ કરતા કેટલા $(\%)$ ટકા $SO_2Cl_2$ નુ વિધટન થશે ?
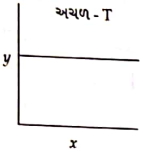
- 9આપેલ આલેખ પ્રક્રિયાની ગતિકી દર્શાવે છે.View Solution
શૂન્ય અને પ્રથમક્રમ પ્રક્રિયા માટે $y$ અને $x$ અક્ષો અનુક્રમે...
- 10$2O_3 \rightarrow 3O_2$ રાસાયણિક પ્રક્રિયા નીચે મુજબ દર્શાવી છે. તો દર નિયમ સમીકરણ..... થશે.View Solution
$ O_3 $ $\rightleftharpoons$ $ O_2 + O$ ...... (ઝડપી) ;
$O + O_3 \rightarrow 2O_2$ ...... (ધીમી)