અર્ધવાહકમાં ઇલેકટ્રોન અને હોલની સંખ્યા ઘનતા $8 \times 10^{18}/m^3$ અને $5 \times 10^{18}/m $છે,ઇલેકટ્રોન અને હોલની મોબિલીટી $2.3 m^2/volt-sec$ અને $0.01 m^2/volt-sec$ છે,તો અર્ધવાહક......
Diffcult
a
\(n_e =8 × 10^{18} m^{-3}, nh = 5×10^{18 } m^{-3}\)
\(n_e =8 × 10^{18} m^{-3}, nh = 5×10^{18 } m^{-3}\)
\( \mu_e = 2.3 m^2 /VS, \mu h = 0.01 m^2/V_S\)
અહીં, \(n_e > n_h\) હોવાથી અર્ધવાહક \(N\) પ્રકારનો હશે.
વાહકતા \(\sigma = \frac{1}{\rho } = e ({n_e}{\mu _e} + {n_h}{\mu _h}) \)
\(\therefore \rho = \frac{1}{{e ({n_e}{\mu _e} + {n_h}{\mu _h})}} = \frac{1}{{1.6 \times {{10}^{ - 19}}((8 \times {{10}^{18}} \times 2.3) + (5 \times {{10}^{18}} \times 0.01))}}\)
\( = 0.34\; \Omega m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
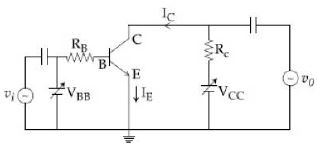
- 1નીચે આપેલ આકૃતિમાં $V_{BB}$ ઉદગમ $0$ થી $5.0 \,V$ સુધી બદલાય છે, ,$V_{CC} = 5\,V,$ $\beta _{dc} = 200,\,$ અને $\,R_B = 100,\,k\Omega ,\,\,R_C = 1\,k\Omega $ અને $V_{BE}=1.0\, V$ છે. ટ્રાન્ઝિસ્ટર સંતૃપ્ત સ્થિતિમાં પહોંચે તે માટે લઘુત્તમ બેઇઝ પ્રવાહ અને ટ્રાન્ઝિસ્ટર સંતૃપ્ત સ્થિતિમાં પહોંચે તે માટેનો ઇનપૂટ (આદાન) વોલ્ટેજ અનુક્રમે _________ થશેView Solution
- 2$P$-પ્રકારના જર્મેનિયમ અર્ધવાહક બનાવવા કઇ અશુદ્વિ ઉમેરવી પડે?View Solution
- 3$Ga-As-P$ જેવા અર્ધવાહકમાંથી $LED$ બનાવવામાં આવે છે. $LED$ નો બેન્ડગેપ $1.9\, eV$ છે, તો તેના દ્વારા ઉત્સર્જાતા પ્રકાશની તરંગલંબાઈ અને રંગ કેવો હશે?View Solution
$\left[ h =6.63 \times 10^{-34} \;Js \right.$ and $\left. c =3 \times 10^{8} \;ms ^{-1}\right]$
- 4View Solutionદોલક એ નીચેનામાંથી કયું એમ્પ્લિફાયર છે?
- 5$n-$ પ્રકારના સિલિકોન માટે નીચેના વિધાનોમાંથી કયું સાચું છે?View Solution
- 6બુલિયન સમીકરણ $\overline A .\overline B \,\, = \,\,...$View Solution
- 7અર્ધતરંગ રેક્ટિફાયર $1 K$ $\Omega$ નો ભાર વિદ્યુત પ્રવાહ આપે છે. વોલ્ટેજ $220V $ છે, ડાયોડના પ્રતિરોધકને અવગણતા, રિપલ વોલ્ટેજ $(rms)$ ની કિંમત ....$volt$ છે.View Solution
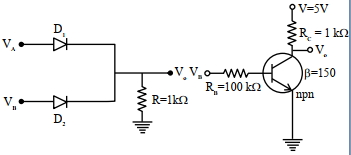
- 8જો ${V}_{{A}}$ અને ${V}_{{B}}$ ઈનપુટ વૉલ્ટેજ ($5\, {V}$ અથવા $0\, {V}$ ) અને ${V}_{0}$ આઉટપુટ વૉલ્ટેજ હોય, તો આપેલ $(A)$ અને $(B)$ પરિપથમાં દર્શાવેલ ગેટ કયા હશે?View Solution
$(A)\quad\quad\quad\quad(B)$
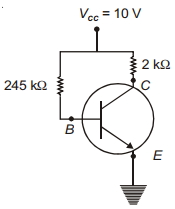
- 9$CE$ ટ્રાન્ઝીસ્ટર સર્કીટમાં બેસ પ્રવાહ $40 \,\mu \,A$ છે. તો $V_{B E}$ એView Solution
- 10એક કોમન એમીટર પરિપથમાં ટ્રાન્ઝિસ્ટરના કલેકટરને અચળ $ V_C=1.5 \;V$ પર એવી રીતે રાખેલ છે કે જેથી બેઝ પ્રવાહમાં $100 \;\mu A$ થી $150\;\mu A$નો ફેરફાર કરતાં કલેકટર પ્રવાહમાં $5 \;mA$ થી $10\; mA$ નો ફેરફાર મળે છે. આ ટ્રાન્ઝિટર માટે $\beta $ કેટલો હશે?View Solution
