બાલટીમાં રહેલ પાણીમાં તરતા એક લાકડાના બ્લોકનું $\frac{4}{5}$ ભાગનું કદ પાણીમાં ડૂબેલું છે.જ્યારે બાલટીમાં થોડુક ઓઇલ નાખવામાં આવે ત્યારે બ્લોકનું અડધું કદ પાણીમાં અને અડધું ઓઇલમાં દેખાય છે તો ઓઇલની સાપેક્ષ ઘનતા કેટલી હશે?
JEE MAIN 2019, Diffcult
c
\(In\,{1^{st\,}}\,situation\)
\(In\,{1^{st\,}}\,situation\)
\({V_b}{\rho _b}g = {V_s}{\rho _w}g\)
\(\frac{{{V_s}}}{{{V_b}}} = \frac{{{\rho _b}}}{{{\rho _w}}} = \frac{4}{5}\) \(...\left( i \right)\)
Here \(V_b\) is volume of block
\(V_s\) is submerged volume of block
\({\rho _b}\) is density of block
\({\rho _w}\) id density of water \(\& \) Let \({\rho _0}\) is density of oil
Finally in equilibrium condition
\({V_b}{\rho _b}g = \frac{{{V_b}}}{2}{\rho _0}g + \frac{{{V_b}}}{2}{\rho _w}g\)
\(2{\rho _b} = {\rho _0} + {\rho _w}\)
\( \Rightarrow \frac{{{\rho _0}}}{{{\rho _w}}} = \frac{3}{5} = 0.6\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાત્રના તળિયે $1 \,cm^{2}$ આડછેદવાળું છિદ્ર છે,પાત્રમાં $70\, cm^{3}/sec$ ના દરથી પાણી નાખતાં મહત્તમ ........ $cm$ ઊંચાઇ સુઘી પાણી ભરી શકાય.View Solution
- 2બે નાના સમાન દળના અને $\rho_{1}$ અને $\rho_{2}\left(\rho_{1}=8 \rho_{2}\right)$ ઘનતા ધરાવતા ગોળાની ત્રિજ્યા અનુક્રમે $1\; mm$ અને $2\; mm$ છે. તે બંનેને એક $\eta$ શ્યાનતાગુણાંક વાળા અને $0.1{\rho}_{2} $ ઘનતા ધરાવતા પ્રવાહીમાં (સ્થિર સ્થિતિમાંથી) પાડવામાં આવે, તો તેમના ટર્મિનલ વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 3જો પાઈપમાંથી વહન પામતા પાણીની ઝડપ $2 \,m / s$ હોય તો તેની એકમ કદ દીઠ ગતિ ઊર્જા ......... $J/m^3$View Solution
- 4સબમરીન દરિયામાં $d_1$ ઊંડાઈએ $5.05\times 10^6\,Pa$ દબાણ અનુભવે છે.જ્યારે તે $d_2,$ ઊંડાઈએ જાય ત્યારે તે $8.08\times 10^6\,Pa$ દબાણ અનુભવે તો $d_2 -d_1$ લગભગ ........ $m$ હશે? (પાણીની ઘનતા $= 10^3\,kg/m^3$ અને ગુરુત્વ પ્રવેગ $= 10\,ms^{-2}$ )View Solution
- 5$P$ પમ્પ દ્વારા $ d $ ઘનતા ધરાવતું પાણી બીજા પાત્રમાં લઇ જવાથી થતું કાર્યView Solution
- 6$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન કદ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution
- 7$A $ અને $B $ પદાર્થો પાણીમાં તરે છે,$A$ પદાર્થનું $\frac{1}{2}$ કદ પાણીમાં ડુબેલું અને $B $ પદાર્થનું $\frac{1}{4}$કદ પાણીની બહાર છે,તો ઘનતાનો ગુણોત્તર કેટલો થાય?View Solution
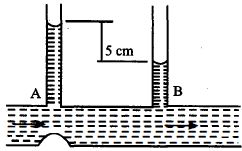
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે મેનોમીટરની બે નળી વચ્ચેનો તફાવત $5\, cm$ છે. $A$ અને $B$ નળીના આડછેડનું ક્ષેત્રફળ અનુક્રમે $6\, mm^2$ અને $10\, mm^2$ છે.તો નળીમાં પાણી ......... $ cc/s$ દરથી વહન કરતું હશે?$(g\, = 10\, ms^{-2})$View Solution
- 9આકૃતિમાં $2.0\,cm ^2$ આડછેદનું ક્ષેત્રફળવાળા પિસ્ટન દ્વારા નળીમાંથી પ્રવાહી ધકેલાતુ દર્શાવેલ છે. નળીના બાહ્ય છેડાનું આડછેદનું ક્ષેત્રફળ $10\,mm ^2$ છે.જો પિસ્ટનને $4\,cm\,s ^{-1}$ જેટલી ઝડપથી ધકેલવામા આવે, તો બહાર જતા પ્રવાહીની ઝડપ ........ $cm\,s ^{-1}$ છે.View Solution

- 10એક બંધ નળી સાથે જોંડેલ દબાણ-મીટરમાં $4.5 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ નું અવલોકન મળે છે. વાલ્વ ચાલુ કરતાં, પાણી વહેવાનું ચાલુ થાય છે અને દબાણ-મીટરમાં અવલોકન ઘટીને $2.0 \times 10^4 \mathrm{~N} / \mathrm{m}^2$ થાય છે. પાણીનો વેગ $\sqrt{\mathrm{V}} \mathrm{m} / \mathrm{s}$ માલૂમ પડે છે. $\mathrm{V}$ નું મૂલ્ય છે.View Solution
