[પાણીનું પૃષ્ઠતાણ ${T}=7.3 \times 10^{-2} \, {Nm}^{-1}$, સંપર્કકોણ $=0, {g}=10\, {ms}^{-2}$ અને પાણીની ઘનતા $\left.=1.0 \times 10^{3} \,{kg} \,{m}^{-3}\right]$
We have \(P_{A}=P_{B}\). [Points \(A\) \(\&\) \(B\) at same horizontal level]
\(\therefore \mathrm{P}_{\mathrm{atm}}-\frac{2 \mathrm{~T}}{\mathrm{r}_{1}}+\rho \mathrm{g}(\mathrm{x}+\Delta \mathrm{h})=\mathrm{P}_{2 \mathrm{tm}}-\frac{2 \mathrm{~T}}{\mathrm{r}_{2}}+\rho g \mathrm{x}\)
\(\therefore \rho g \Delta \mathrm{h}=2 \mathrm{~T}\left[\frac{1}{\mathrm{r}_{1}}-\frac{1}{\mathrm{I}_{2}}\right]\)
\(=2 \times 7.3 \times 10^{-2}\left[\frac{1}{2.5 \times 10^{-3}}-\frac{1}{4 \times 10^{-3}}\right]\)
\(\therefore \Delta \mathrm{h}=\frac{2 \times 7.3 \times 10^{-2} \times 10^{3}}{10^{3} \times 10}\left[\frac{1}{2.5}-\frac{1}{4}\right]\)
\(=2.19 \times 10^{-3} \mathrm{~m}=2.19 \mathrm{~mm}\)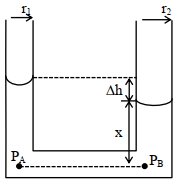
Download our appand get started for free
Similar Questions
- 1કેશનળીની $l$ લંબાઇ પાણીમાં ડુબાડતાં $h$ ઊંચાઇ સુધી પાણી ઉપર આવે છે,જો કેશનળીનો નીચેનો છેડો બંધ કરીને કેશનળીને બહાર કાઢી લેવામાં આવે છે.હવે છેડો ખુલ્લો કરી દેવામાં આવે,ત્યારે કેશનળીમાં પાણીની ઊંચાઇView Solution
- 2જો સાબુના પરપોટાની અંદર વધારાના દબાણને $2\; mm$ ઊંંચાઈના તેલના સ્તંભ વડે સંતુલિત કરવામાં આવે છે તો પછી સાબુના દ્રાવણનું પૃષ્ઠતાણ કેટલું હશે? ($r=1\; cm$, તેલની ઘનતા = $\left.0.8 \;g / cm ^3\right)$View Solution
- 3$4\,cm$ ત્રિજ્યાનો સાબુનો પરપોટો બીજા $6\,cm$ ત્રિજ્યાના પરપોટામાં તેને સંપર્ક કર્યા સીવાય ફસાયેલ છે.$P_2$ એ અંદરના પરપોટાની અંદરનું દબાણ અને $P_0$ એ બહારના પરપોટાની બહારનું દબાણ છે.બીજા એક પરપોટોની ત્રિજ્યા જેની અંદર બહારના દબાણનો તફાવત $P_2 - P_0$ હોય? ....... $cm$View Solution
- 4એક પોલા ગોળામાં નાનું છિદ્ર હોય છે, જ્યારે તેની પાણીની સપાટીની નીચે $40 \,cm$ ઊંડાઈએ લઈ જવામાં આવે છે, ત્યારે જ તેમાં પાણી દાખલ થાય છે. પાણીનું પૃષ્ઠતાણ $0.07 \,N / m$ છે. છિદ્રનો વ્યાસ ........... $mm$.View Solution
- 5કેશનળીને પાણીમાં ડુબાડતાં $h$ ઊંચાઇ સુધી પાણી ઉપર આવે છે.જો અડધી ત્રિજયાની કેશનળીને પાણીમાં ડુબાડતાં કેટલી ઊંચાઇ સુધી પાણી ઉપર આવે?View Solution
- 6પ્રવાહીનું પૃષ્ઠતાણ $5 \,N / m$ છે. જો ફિલ્મને $0.02 \,m ^2$ ક્ષેત્રફળ ધરાવતી રિંગમાં રાખવામાં આવે છે તો તેની પૃષ્ઠ ઊર્જા ......... $J$ છે?View Solution
- 7$2\,m$ લંબાઇની લાકડાની સળી પાણી પર તરે છે, પાણીનું પૃષ્ઠતાણ $0.07\, N/m$ છે.સળીની એક બાજુ $0.06\, N/m$ પૃષ્ઠતાણ ધરાવતું સાબુનું દ્રાવણ નાખતાં તેના પર પરિણામી બળ ......... $N$ લાગે.View Solution
- 8$0.8$ અને $0.6 $ સાપેક્ષ ઘનતા અને $60\, dyne/cm$ અને $50 \,dyne/cm$ પૃષ્ઠતાણ ધરાવતા પ્રવાહીમાં સમાન કેશનળી ડુબાડતાં પ્રવાહીની ઊંચાઇનો ગુણોત્તર કેટલો થાય?View Solution
- 9પાણીમાં રહેલા પરપોટાનું દબાણ $P_1$. છે,સમાન ત્રિજયા ધરાવતા ટીપાંનું દબાણ $P_2$ છે,તોView Solution
- 10$r$ ત્રિજ્યાના નાના $729$ ટીપાં ભેગા કરીને એક મોટું $R$ ત્રિજ્યાનું ટીપું બનાવવામાં આવે તો દરેક નાના ટીપાની ત્રિજ્યા કેટલી હશે?View Solution
