ચાકગતિ કરતો નળાકાર \(-A \ \ 50 \) પરિભ્રમણ પ્રતિ સેકન્ડની કોણીય વેગથી ગતિ કરે છે.
તેનો કોણીય વેગ \(\omega_{OA}=50 \) પરિભ્રમણ પ્રતિ સેકન્ડ જ્યારે નળાકાર \(B\) સ્થિર સ્થતિમાં છે.
તેનો કોણીય વેગ \(\omega_{OB}=0 \) પ્રતિભ્રમણ પ્રતિ સેકન્ડ સંપર્કમાં આવ્યા બાદ,
નળાકાર - \(A\) અને નળાકાર - \(B\) અનુક્રમે કોણીય પ્રતિપ્રવેગ અને કોણીય પ્રવેગનો માનાંક \(1\ rad s^{-2}\) છે.
ધારો કે \(t\ s\) જ બાદ બંનેનો કોણીય વેગ \(\omega\) થાય.
નળાકાર \({\text{ - A}}\) માટે
\(\omega = \,\,{\omega _0} + \alpha t\,\,\,\,\,\therefore \,\frac{{\omega - {\omega _0}}}{\alpha } = t\,\,\,\)
\(\therefore t = \frac{{\omega - 50}}{{ - 1}} = (50 - \omega )\,s\,\,\,.......(\,1)\)
નળાકાર \({\text{ - B}}\) માટે ,
\(\omega = \,\,{\omega _0} + \alpha t\,\,\,\,\therefore t = \frac{{\omega - {\omega _0}}}{\alpha } = \frac{{\omega - 0}}{1} = \omega \,\,\,.....(\,2)\)
સમીકરણ (1) અને સમીકરણ (2) ને સરખાવતાં, \(\omega = 50-\omega\),
\(2\omega=50\), \(\omega=25\) પરિભ્રમણ પ્રતિ સેકન્ડ
વે, સમીકરણ (2) મુજબ \(t=\omega\)
\(t=25\ s\)
Download our appand get started for free
Similar Questions
- 1$M $ દળ અને $ R$ ત્રિજ્યાના વર્તૂળાકાર વાયરની તેના વ્યાસ જડત્વની ચાકમાત્રા ....... છે.View Solution
- 2સ્થિર સ્થિતિમાંથી એક રિંગ ઉપર ટૉર્ક લગાડતાં, તે અચળ કોણીય વેગ $8\ rad s^{-2}$ ની અસર હેઠળ ચાકગતિ શરૂ કરે છે. આ રિંગ $5\ s$ માં કેટલાં પરિભ્રમણ કરશે છઠ્ઠી સેકન્ડમાં આ રિંગ કેટલા પરિભ્રમણ કરશે ? જો $6\ s$ બાદ રિંગ ઉપર લાગતું ટૉર્ક શૂન્ય થઈ જાય, તો સાતમી સેકન્ડમાં આ રિંગ કેટલાં પરિભ્રમણ કરશે ?View Solution
- 3જો કુલ ગતિ ઊર્જાનો $50\%$ ચાક ગતિ ઊર્જા હોય તો તે પદાર્થ .......... છે.View Solution
- 4નિયમિત સળિયાનું દળ $ M$ અને લંબાઈ $ ℓ$ સળિયાને લંબ કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા $ I$ છે. સળિયાના છેડામાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 5View Solutionઢોળાવવાળા સમતલ પર અમુક ઉંચાઈ નળાકાર ચઢે છે અને પછી ગબડીને નીચે આવે છે. (સમગ્ર ગતિ દરમિયાન સરકતો નથી.) નળાકાર પર લાગતા ઘર્ષણ બળની દિશા કઈ છે.
- 6બાજુ $b$ ધરાવતાં ચોરસનાં ચાર ખૂણાઓ ઊપર $m$ દળ ધરાવતાં અને $a$ ત્રિજ્યા ધરાવતાં ચાર એક સરખા ઘન ગોળા ગોઠવેલા છે. ચોરસની એક બાજુ કે જ્યાં પરિભ્રમણ અક્ષ ચોરસના સમતલને લંબ હોય તેને સાપેક્ષ જડત્વની ચાકમાત્રા ............... હશે.View Solution
- 7એક જાડી દીવાલ નો પોલા ગોળાની બાહ્ય ત્રિજ્યા $R_0$ છે. તે કોઈ ઢોળાવ પર સરક્યાં વગર ગબડે છે અને તળિયે પહોંચતા તેની ઝડપ $v_0$ છે. ઢોળાવને મીણવાળો કરવામાં આવે છે કે જેથી પ્રાયોગિક ધોરણે તે ઘર્ષણરહિત થઈ શકે અને ગોળા ને ગબડાવ્યા વગર સરકતો જોઈ શકાય. હવે તળિયે તેની ઝડપ $5{v_0}/4$ . તો પોલા ગોળા ના કેન્દ્રમાથી પસાર થતી કોઈ અક્ષને અનુલક્ષીને ચક્રવર્તનની ત્રિજ્યા શું થશે?View Solution
- 8એક સમતલ સમક્ષીતિજ સાથે $ 30^°C$ ના કોણ બનાવે છે. આ સમતલ પરથી એક ગોળો સરક્યા વિના ગબડે તો આ ગોળાનો રેખીય પ્રવેગ કેટલો હશે?View Solution
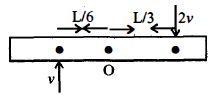
- 9લંબાઈ $L$ અને દળ $8\,m$ ની એક નિયમિત પાતળી પટ્ટી ને લીસ્સા સમક્ષિતિજ ટેબલ પર મૂકેલી છે. બે સૂક્ષ્મ દળો $m$ અને $2\,m$ સમાન સમક્ષિતિજ સમતલ માં પટ્ટીની પરસ્પર વિરુદ્ધ બાજુઓ તરફ અનુક્રમે $2v$ અને $v$ વેગથી ગતિ કરે છે. તે દળો પટ્ટી સાથેના સંઘાત બાદ પટ્ટીના કેન્દ્રથી અનુક્રમે $\frac{L}{3}$ અને $\frac{L}{6}$ અંતરે પટ્ટી પર ચોંટી જાય છે. પટ્ટી સંઘાતના પરિણામના ભાગરૂપે તેના દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને ભ્રમણ શરૂ કરે છે તો પટ્ટીનો કોણીય વેગ કેટલો હશે?View Solution
- 10$1\ kg$ નો એક પદાર્થ $2\ ms^{-1}$ જેટલા રેખીય વેગથ ધન $X -$ અક્ષને સમાંતર ગતિ કરી રહ્યો છે. આ ગતિ દરમિયાન ઉગમબિંદુથી તેનું લઘુતમ અંતર $ 12\ cm $ થાય છે, તો આ પદાર્થનું ઉગમબિંદુને અનુલક્ષીને કોણીય વેગમાન ....... $Js$View Solution
