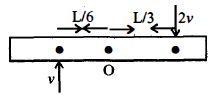
Linear momentum is conserved
\(2 m v-2 m v=(2 m+m+M) V_{c m}\)
\(\Rightarrow V_{c m}=0\)
Angular momentum is conserve
\(2 m v \frac{L}{6}+2 m v \times \frac{L}{3}+0=I w\) \(...(i)\)
\(I=\mathrm{M.I.}\) of rod \(+\mathrm{M.I.}\) of mass \(2 \mathrm{m}+\mathrm{M.I}\) of mass \(\mathrm{m}\)
\(=\frac{8 m L^{2}}{12}+2 m\left(\frac{L}{6}\right)^{2}+m\left(\frac{L}{3}\right)^{2}\)
\(=m L^{2}\left(\frac{2}{3}+\frac{1}{18}+\frac{1}{9}\right)=\frac{5}{6} m L^{2}\)
eqn \((1)\) becomes
\(\left(\frac{m v L}{3}+\frac{2}{3} m v L\right)=\frac{5}{6} m L^{2} w\)
\(\frac{m L}{3}(V+2 v)=\frac{5}{6} m L^{2} w\)
\(\frac{6 V}{5 L}=w\)
Download our appand get started for free
Similar Questions
- 1જ્યારે એક ઓટોમોબાઇલ $1800$ પરિભમણ પ્રતિ મિનિટ થી ભ્રમણ કરતું હોય ત્યારે તે $100\ kW$ નો પાવર ઉત્પન્ન કરે છે તો તેમાં કેટલું ટોર્ક ($N-m$ માં) લાગતું હશે?View Solution
- 2સમાન તારમાથી બનાવેલ એક સમબાજુ ત્રિકોણ $ ABC$ ના શિરોબિંદુ $A $ પાસે બે સમાન ગોળીઓ રાખેલ છે. ત્રિકોણને $AO$ અક્ષને અનુલક્ષીને ભ્રમણ કરાવવામાં આવે છે. અને પછી આ ગોળીઓને સ્થિર સ્થિતિમાંથી એક સાથે અનુક્રમે $ AB$ અને $ AC$ ની દિશામાં ગતિ કરાવવામાં આવે છે, (જુઓ આકૃતિ) તો ઘર્ષણબળને અવગણતાં, ગોળીઓની અધોદિશામાંની ગતિ દરમિયાન કઇ રાશિઓનું સંરક્ષણ થશે ?View Solution

- 3$(1)$ રિંગView Solution
$(2)$ તકતી
$(3)$ ઘન નળાકાર
$(4)$ ઘન ગોળો
બધા જ પદાર્થોના દળ $m$ અને ત્રિજ્યા $R$ છે તેમને સમાન ઢાળ પરથી મુક્તા તે ગબડીને નીચે તળિયે આવે છે. તો પ્રથમ તળિયે કયા નંબરનો પદાર્થ આવશે?
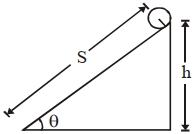
- 4$M $ દળ અને $R$ ત્રિજ્યાવાળો નક્કર નળાકાર $ L$ લંબાઈના ઢાળ પરથી સરક્યા સિવાય ગબડે છે. ઢાળની ઊચાઈ $h$ છે. જ્યારે નળાકાર ઢાળના તળિયે પહોંચે ત્યારે તેના દ્રવ્યમાન-કેન્દ્રનો વેગ કેટલો હશે ?View Solution
- 5એક પૈડું $ 3\ rad s^{-2}$ કોણીય પ્રવેગ અને પ્રારંભિક કોણીય વેગ $2\ rad s^{-1}$ થી ગતિ કરે છે. $2 \ s $ બાદ તેનું કોણીય સ્થાનાંતર ....... $\ rad$ હશે .View Solution
- 6ઉદગમબિંદુ થી $(3\hat i + 2\hat j - 4\hat k)$ $m$ અંતરે $(2\hat i - 4\hat j + 2\hat k)$ $N$ બળ લાગે તો ટોર્ક નું મૂલ્ય ....... $ N-m$ થાય.View Solution
- 7$M $ દળ તથા $ L$ લંબાઈના સળીયાની તેના એક છેડેથી $L/4$ અંતરે સળીયાની લંબાઈને લંબ અક્ષની આસપાસ જડત્વની ચાકમાત્રા = .....View Solution
- 8$l$ બાજુવાળી અને એકમ ક્ષેત્રફળ દીઠ દળ $\mu $ ધરાવતી ચોરસ તકતીના કેન્દ્રમાંથી અને સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 9$m$ દળના કણની સમય $t$ સાથે નીચે મુજબ ગતિ કરે છે.View Solution
$\overrightarrow{{r}}=10 \alpha {t}^{2}\, \hat{{i}}+5 \beta({t}-5)\, \hat{{j}}$
જ્યાં $\alpha$ અને $\beta$ પરિમાણવાળા અચળાંક છે. કણનું કોણીય વેગમાન ${t}=0$ સમયે હોય તેટલું ફરીથી $t=$ .....$seconds$ સમયે થશે.
- 10$M$ દળ અને $R$ ત્રિજયાની તકતીના પરિધના સ્પર્શકમાંથી પસાર થતી અને વ્યાસને સમાંતર અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
