બે તકતી તેની અક્ષને અનુલક્ષીને સમાન દિશામાં ભ્રમણ કરે છે.પ્રથમ તકતીની જડત્વની ચાક્માત્રા $0.1 \;kg \cdot m ^{2}$ અને કોણીય ઝડપ $10\; rad \,s^{-1}$ છે,બીજી તકતીની જડત્વની ચાક્માત્રા $0.2 \;kg - m ^{2}$ અને કોણીય ઝડપ $5\; rad \,s ^{-1}$ છે,તેમની અક્ષને જોડીને એક તકતી બનાવતા તંત્રની ગતિઊર્જા ...........$J$
JEE MAIN 2020, Diffcult
Download our app for free and get started
d
Both discs are rotating in same sense
Both discs are rotating in same sense
Angular momentum conserved for the system
i.e. \(\quad L _{1}+ L _{2}= L _{\text {final }}\)
\(I _{1} \omega_{1}+ I _{2} \omega_{2}=\left( I _{1}+ I _{2}\right) \omega_{ f }\)
\(0.1 \times 10+0.2 \times 5=(0.1+0.2) \times \omega_{f}\)
\(\omega_{ f }=\frac{20}{3}\)
Kinetic energy of combined disc system
\(\Rightarrow \frac{1}{2}\left( I _{1}+ I _{2}\right) \omega_{ f }^{2}\)
\(=\frac{1}{2}(0.1+0.2) \cdot\left(\frac{20}{3}\right)^{2}\)
\(=\frac{0.3}{2} \times \frac{400}{9}=\frac{120}{18}=\frac{20}{3} J\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $ m$ દળ, $r $ જેટલી ત્રિજ્યા અને $\omega_0$ જેટલી કોણીય આવૃત્તિ ધરાવતી રિંગને ખરબચડી સપાટી પર રાખેલ છે. રિંગના કેન્દ્રનો પ્રારંભિક વેગ શૂન્ય છે. જ્યારે રિંગ સરકવાનું બંધ કરે ત્યારે તેના કેન્દ્રનો વેગ કેટલો હશે ?View Solution
- 2$M$ દળ અને $R$ ત્રિજયાવાળો નકકર નળાકાર $L$ લંબાઇના ઢાળ પરથી સરકયા સિવાય ગબડે છે.ઢાળની ઊંચાઇ $h$ છે.જયારે નળાકાર ઢાળના તળિયે પહોંચે ત્યારે તેના દ્રવ્યમાન-કેન્દ્ર નો વેગ કેટલો હશે?View Solution
- 3સમાન દળ અને ત્રિજ્યા ધરાવતાં ચાર વસ્તુઓની જડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ દર્શાવાય છે.View Solution
$I _{1}=$ પાતળી રિંગની તેના વ્યાસને અનુલક્ષીને $M.I.,$
$I _{2}=$ વર્તુળાકાર તકતીની તેના કેન્દ્રમાંથી પસાર થતી અને તકતીને લંબ અક્ષને અનુલક્ષીને $M.I.$
$I_{3}=$ ઘન નળાકારની તેની અક્ષને અનુલક્ષીને $M.I.$ અને
$I _{4}=$ ઘન ગોળાની તેના વ્યાસને અનુલક્ષીને $M.I.$
તો :
- 4$ℓ$ લંબાઈનો બાજુનું માપ વાળા ચોરસના ચારેય ખૂણા પર $m$ દળના ચાર ગણો મૂકેલા છે. તેના કેન્દ્રમાંથી પસાર થતી અને ચોરસના સમતલને લંબ અક્ષ પર તંત્રની ચક્રાવર્તનની ત્રિજ્યા ......... છે.View Solution
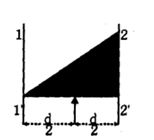
- 5View Solutionઆકૃતિમાં કઇ અક્ષ પર કોણીય પ્રવેગ વધુ થશે અને બળ ત્રિકોણ ફ્રેમના મધ્યબિંદુ પર લાગે છે.
- 6મોટરને બંધ કરવામાં આવે ત્યારે, $M kg$ દળ અને $R$ મીટર ત્રિજ્યાની એક તકતી $\omega \,rad / s$ ની કોણીય ઝડપે ભ્રમણ કરે છે. અક્ષીય ધર્ષણને અવગણતા, $t$ સમય માં, વ્હીલને સ્થિર કરવા માટે વ્હીલ પર સ્પર્શકીય રીતે કેટલું બળ લગાડવું જોઈએે ?View Solution
- 7એક ધરી પર રહેલ પૈડાની જડત્વની ચાકમાત્રા $3 \times 10^2\ kg m^2$ છે તથા અચળ કોણીય ઝડપ $4.6\ rad\ s^{-1}$ છે. જો પૈડા પર લાગતું પ્રતિટોર્ક $6.9\times10^2\ N.m $ હોય તો ...... (સેકન્ડ) સમયમાં પૈડુ ઉભું રહી જાય ?View Solution
- 8ચાર સમાન બિંદુવત $T$ દળ (દરેકનું દળ $ m$) ને તકતીના પરીઘ પર મૂકેલા છે. આ તકતીનું દળ $M $ અને ત્રિજ્યા $R$ છે. કેન્દ્ર $O$ ને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
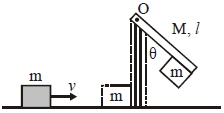
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $m =1\, kg$ દળનો એક પદાર્થ $v=6\, m / s$ જેટલા વેગથી એક ઘર્ષણરહિત સપાટી પર ગતિ કરીને એક સળિયા સાથે અથડાયને તેની સાથે જોડાય જાય છે. આ સળિયો $O$ બિંદુ સાથે જડેલ છે અને અથડામણના કારણે તે $\theta$ ખૂણો બનાવે છે. જો સળિયાનું દળ $M =2 \,kg $ અને લંબાઈ $l=1\, m $ હોય તો $\theta$ ખૂણાનું મૂલ્ય કેટલું હશે?View Solution
$(\left.g=10 \,m / s ^{2}\right)$
- 10કોઈ સળિયાને લંબ તેના કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{1}{{12}}\,M{L^2}$ (જ્યાં $M$ એ સળિયાનું દળ અને $L$ એ સળિયાની લંબાઈ) છે.સળિયાને વચ્ચેથી વાળવામાં આવે છે કે જેથી તેના બંને ભાગ $60^o$ નો ખૂણો બનાવે. તો તે જ અક્ષને અનુલક્ષીને વળેલા સળિયાની જડત્વની ચાકમાત્રા શું થાય?View Solution