કોઈ સળિયાને લંબ તેના કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{1}{{12}}\,M{L^2}$ (જ્યાં $M$ એ સળિયાનું દળ અને $L$ એ સળિયાની લંબાઈ) છે.સળિયાને વચ્ચેથી વાળવામાં આવે છે કે જેથી તેના બંને ભાગ $60^o$ નો ખૂણો બનાવે. તો તે જ અક્ષને અનુલક્ષીને વળેલા સળિયાની જડત્વની ચાકમાત્રા શું થાય?
AIIMS 2006, Medium
Download our app for free and get started
b
We know that for a body, moment of inertia
We know that for a body, moment of inertia
\(M.I. = \sum {m\,{r^2}} \)
Now, bending of rod does not alter the distribution of individual particle, the body
is made of, so the value of \(\sum {m\,{r^2}} \) will not change. Hence the changed moment of inertia of the body will be \(\frac{1}{{12}}\,\,M{L^2}\)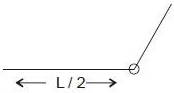
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીની કોણીય ઝડપ $\omega_{1}$ છે. બીજી $\frac{ R }{2}$ ત્રિજ્યા અને $M$ દળ ધરાવતી તકતી તેના પર મુક્તા નવી કોણીય ઝડપ $\omega_{2}$ છે.શરૂઆતની ઊર્જાનો વ્યય થાય તો $p=.......$View Solution
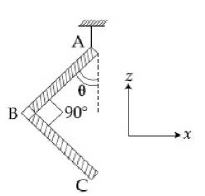
- 2એકસમાન દળ ઘનતા ધરાવતા પાતળા સળીયામાંથી $L- $આકારની એક વસ્તુ બનાવવામાં આવે છે જેને દોરી વડે આકૃતિમાં બતાવ્યા પ્રમાણે લટકાવવામાં આવી છે. જો $AB = BC$ હોય અને $AB$ થી અધોદિશામાં બનતો કોણ $\theta $ હોય તોView Solution
- 3$0.4\, kg$ દળ અને $100\, cm$ ત્રિજ્યા ધરાવતી નિયમિત વર્તુળાકાર તકતીના સમતલને લંબ તેના કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ...... $kg\, m^2$ થશે?View Solution
- 4$m$ અને $M$ $(M>m)$ ના દળોનું દ્રવ્યમાન કેન્દ્રView Solution
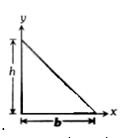
- 5View Solutionઆકૃતિમાં દર્શાવેલ ત્રિકોણના દ્રવ્યમાન-કેન્દ્રના યામ ....... .
- 6એક $2 R$ ત્રિજ્યાની વર્તુળાકાર તકતીમાંથી $R$ ત્રિજ્યાની તકતી એવી રીતે કાપવામાં આવે છે કે જેથી બંને વર્તુળના પરિધ પરસ્પર સ્પર્શે. નવી તકતીનું દ્રવ્યમાન કેન્દ્ર મોટા વર્તુળના કેન્દ્રથી $\frac{\alpha}{R}$ અંતરે છે. તો $\alpha$ ની કિંમત કેટલી હશે?View Solution
- 7$2\,kg$ દ્રવ્યમાન ધરાવતો ધનગોળો સમક્ષિતિજ પૃષ્ઠ પર $2240\,J$ ગતિઉર્જા સાથે શુદ્ધ લોટણ ગતિ કરે છે. તો ગોળાના કેન્દ્રનો વેગ $............ms ^{-1}$ હશે.View Solution
- 8જો $\overrightarrow{ F }=3 \hat{i}+4 \hat{j}-2 \hat{k}$ બળ એ $2 \hat{i}+\hat{j}+2 \hat{k}$ સ્થાન સદીશ ધરાવતા કણ ઉપર લાગતો હોય, તો ઊગમબિંદુને અનુલક્ષીને ટોર્ક............હશેView Solution
- 9View Solutionચાકગતિ કરતા દઢ પદાર્થના દરેક કણોના ...... હોય છે.
- 10એક $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીનું એકમ ક્ષેત્રફળ દીઠ દળ $\sigma (r) = kr^2$ મુજબ આપવામાં આવે છે જ્યાં $r$ એ તકતીના કેન્દ્રથી અંતર છે.તો તેના સમતલને લંબ અને દ્રવ્યમાન કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution