(d)
after reaching ground aal the potential energy will bw converted to kinrtic enetgy,
for rolling object,\(K \cdot E=\frac{m v^2}{2}+\frac{I w^2}{2}\)
where \(I=\)Moment of inertia \(=\frac{m r^2}{2}\)
\(\omega =\) angular velocity \(= \frac{v}{r}\)
let the two disc have mass \(m\) and \(2m\) and radius \(r\) and \(8r\) for disc \(1.\)
\(PE=KE\)
\(m g h=\frac{m v^2}{2}+\left(\frac{1}{2}\right) \times \frac{m v^2}{2} \times\left(\frac{v}{r}\right)^2\)
\(m g h=\frac{m v^2}{2}+\frac{m v^2}{4}\)
\(m g h=\frac{3 m v^2}{4}\)
\(\therefore v=\sqrt{\frac{4 g h}{3}}\)
similarly for disc \(2\),let the speed be \(v^{\prime}\)
\(2 m g h=\frac{2 m v^{.2}}{2}+\frac{1}{2}\left(2 m \times \frac{64 r^2}{2}\right) \times\left(\frac{v^{\prime}}{64 r^2}\right)\)
\(2 m g h=\frac{3 m v^{\prime 2}}{2}\)
\(v^{\prime}=\sqrt{\frac{4 g h}{3}}\)
Hence the ratio of theair speed will be \(v : v^{\prime}\) \(=1:1\)
Download our appand get started for free
Similar Questions
- 1$1.5 \,m$ ત્રિજ્યા ધરાવતી એક પુલીને (ગરગડી)ને $F=\left(12 t -3 t ^{2}\right) \,N$ જેટલા સ્પર્શીય બળ (જ્યાં $t$ એ સેકન્ડમાં મપાય છે) વડે તેની અક્ષને ફરતે ભ્રમણ કરાવવામાં આવે છે. જો પુલીને તેની ભ્રમણ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $4.5 \,kg m ^{2}$ છે,તો તેની ભ્રમણની દિશા ઉલટાય તે પહેલાં પુલી દ્વારા થતા ભમણોની સંખ્યા $\frac{K}{\pi}$ છે. $K$ નું મૂલ્ય ........... હશે.View Solution
- 2$10\, g$ દળ અને $500\, m/s$ ની ઝડપે એક બુલેટને બારણાંમાં છોડવામાં આવે છે જેથી તે બારણાની વચ્ચે ખૂંચી જાય છે. બારણું $1.0\, m$ પહોળું અને $12\, kg$ વજનવાળું છે. તેનો એક ભાગ જોડેલો છે અને તે તેના શિરોલંબ અક્ષ ને અનુલક્ષીને ઘર્ષણરહિત ભ્રમણ કરે છે. બુલેટ તેમાં ખૂંચે પછી તરત તેની કોણીય ઝડપ કેટલી હશે?View Solution
- 3$X$ અને $Z $ અક્ષ તકતીના સમતલમાં પરસ્પર લંબ છે અને $Y$ અક્ષ તકતીના સમતલને લંબ છે. જો પદાર્થની $X$ અને $Y$ અક્ષ પર જડત્વની ચાકમાત્રા અનુક્રમે $ 30\ kg m^2 $ અને $40\ kg m^2$ ત્યારે $Z$ અક્ષ પર જડત્વની ચાકમાત્રા ....... $kgm^2$ થશે .View Solution
- 4સ્થિર સમક્ષિતિજ તક્તી પોતાની અક્ષની સાપેક્ષે મુક્ત રીતે પરિભ્રમણ કરી શકે છે.જ્યારે તેના પર ટોર્ક લગાવતા તેની ગતિઉર્જા $\theta $ મુજબ $k\theta ^2$ રીતે બદલાય છે,જ્યાં $\theta $ એ ખૂણો છે જેની સાપેક્ષે તે ભ્રમણ કરે છે.જો તેની જડત્વની ચકમાત્રા $I$ હોય તો તકતીનો કોણીય પ્રવેગ કેટલો થાય?View Solution
- 5એક પાતળી $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી રિંગ તેની અક્ષને અનુલક્ષીને $\omega$ કોણીય ઝડપથી ફરે છે. ચાર $m$ દળના પદાર્થને રિંગ પર તેના બે લંબ વ્યાસના છેડે મૂકવામાં આવે છે. રિંગનો કોણીય વેગ કેટલો થાય?View Solution
- 6આ પ્રશ્ન માં વિધાન $1$ અને વિધાન $2$ છે. આપેલ ચાર વિકલ્પોમાથી બંધબેસતો વિકલ્પ પસંદ કરો.View Solution
વિધાન $1$: જો પોતાની અક્ષને અનુલક્ષીને કોણીય ઝડપ $\omega $ થી ભ્રમણ કરતાં પદાર્થની જડત્વની ચાકમાત્રામાં વધારો થાય તો તેના કોણીય વેગ $L$ માં કોઈ પણ ફેરફાર નહિ થાય પણ જો ટોર્ક લગાવેલ નહિ હોય તો ગતિઉર્જા $K$ વધશે.
વિધાન $2$: $L = I\omega $, ભ્રમણ ની ગતિઉર્જા $ = \frac{1}{2}\,I\omega ^2$
- 7એક નિયમિત વર્તુળાકાર ચક્ર પર લાગતું અચળ ટોર્ક $4$ સેકંડ માં તેનાં કોણીય વેગમાનને $A_0$ થી $4 A_0$ માં પરિવર્તીત કરે છે. તો આ ટોર્ક નું મૂલ્ય કેટલું હશે?View Solution
- 8View Solutionબળયુગ્મ કેવી ગતિ ઉત્પન્ન કરે છે
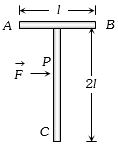
- 9આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.View Solution
- 10એક સમાન જાડાય ધરાવતી $56\ cm$ વ્યાસ વાળી એક વર્તુળાકાર તક્તીમાથી એક બાજુ એ થી $42\ cm$ વ્યાસ વાળો એક ભાગ દૂર કરવામાં આવે તો વધેલા ભાગનું દ્રવ્યમાનકેન્દ્ર ........ $cm$ થાય.View Solution
